Niveauneutrale Modellierung der Ertragsvolatilität von Winterweizen und Silomais auf mehreren räumlichen Ebenen in Deutschland
Level normalized modeling approach of yield volatility for winter wheat and silage maize on different scales within Germany
Journal für Kulturpflanzen, 67 (6). S. 205–223, 2015, ISSN 1867-0911, DOI: 10.5073/JfK.2015.06.01, Verlag Eugen Ulmer KG, Stuttgart
Wetterbedingte Ertragsschwankungen stellen für die Landwirtschaft ein Produktionsrisiko dar. Besonders problematisch sind dabei negative Ertragsanomalien, die sich durch den Klimawandel häufen können. Im Rahmen dieser Studie wurden statistische Ertragsmodelle entwickelt und getestet, mit denen Ertragsanomalien modelliert und fortgeschrieben werden können. Für die Modellierung wurden als winterannuelle Kultur Winterweizen und als sommerannuelle Kultur Silomais als die Kulturen mit dem jeweils größten Anbauumfang in Deutschland ausgewählt. Die Erträge dieser beiden Kulturen wurden auf Landkreisebene modelliert und dann auf der Ebene der Bundesländer, Flusseinzugsgebiete und für Deutschland verglichen. Dazu wurden drei statistische Ansätze verwendet: separate Zeitreihenmodelle, Paneldatenmodelle und Zufallskoeffizientenmodelle. Über die funktionale Form der Cobb-Douglas-Produktionsfunktion wurden relative Änderungen im Vergleich zum Vorjahr (Ertrags- und Faktoranomalien) miteinander in Beziehung gesetzt. Halb- und vierteljährlich summierte Klimavariablen gingen in die Modellbildung ein. Den Klimaeinfluss verzerrende ökonomische Einflüsse wurden von Proxyvariablen quantifiziert. Die Ergebnisse (gemessen am Nash-Sutcliffe Modell-Effizienz-Koeffizienten) der Studie zeigten, dass die methodisch einfachsten separaten Zeitreihenmodelle Ertragsanomalien durchgehend besser (0.81) erklärten als die Paneldatenmodelle (0.72) und auch außergewöhnliche, landkreisindividuelle Ertragsänderungen erfassten. Die Erklärungskraft der Zufallskoeffizientenmodelle lag zwischen den separaten Zeitreihenmodellen und den Paneldatenmodellen (0.78). Durch die Aggregation der Landkreiserträge zu Flusseinzugsgebiets- und Bundesländererträgen wurden höhere Erklärungswerte erreicht (+0.14). Dieser Aggregationseffekt war am höchsten beim Paneldatenmodell für Flusseinzugsgebiete (+0.26). Für beide Kulturen werden ähnliche Erklärungswerte erreicht. Die räumliche Verteilung der Modellparameter spiegelte die vorherrschenden Boden- und Klimaeigenschaften Deutschlands in den unterschiedlichen Entwicklungsperioden wieder. Durch die Normierung sind die Erträge einerseits unabhängig vom technologischen Niveau, andererseits können sie ohne Fehlerkorrektur direkt mit simulierten Wetter- und Klimamodellen kombiniert werden. Durch die grobe zeitliche Einteilung der Klimavariablen lassen sich mit den Modellen robuste Projektionen abgeben. Unsere statistischen Modelle erfassten kollinear verlaufende Faktoren der Ertragsbildung, beispielsweise Schädlinge oder das Anpassungsverhalten der Landwirte an sich ändernde klimatische oder ökonomische Bedingungen. Dadurch konnten sie Praxiserträge besser abbilden als prozessbasierte Modelle. Die geschätzten statistischen Modelle sind geeignet, um Ertragsanomalien für Wetter- und Klimaprojektionen fortzuschreiben. Die separaten Zeitreihenmodelle reproduzierten insgesamt am besten die gemessenen Ertragsänderungen.
Stichwörter: Statistische Ertragsmodelle, Klimafolgen, Winterweizen, Silomais, Volatilität
Weather-related yield volatility is an important production risk for agriculture. Especially, negative yield anomalies could increase through climate change. We develop and investigate statistical crop yield models which can be used to predict crop yield impacts of weather and climate projections. The models are applied to winter wheat and silage maize, which are the most important annual crops as winter and spring crops, respectively, in Germany. The yields of both crops were modelled on county level, but evaluated on federal state, river basin or national level. We use three regression methods: separate time series model, panel data model, and random coefficient model. Within the Cobb-Douglas production function, relative changes (of yield and factor anomalies) are related to each other. To include the conditions of vegetative and generative plant development, we use climate variables summed to quarter- and half-year values. Furthermore, our models are controlled with proxy variables for economic impacts to estimate unbiased climatic parameters. Our study shows that the simple separate time series models explain (measured by the Nash-Sutcliffe model efficiency coefficient) yield anomalies best. They perform generally better (0.81) than the panel data models (0.72) due to a more accurate reproduction of exceptional yield changes at the county level. The random coefficient models performed between the separate time series models and panel data models (0.78). The aggregation of county yields to federal state and river basin yields improves the model accuracy by + 0.14. The aggregation effect is at highest for the panel data model on river basin scale (+0.26). The models for both crops achieve a similar goodness of fit. The spatial distribution of model parameters reflects the prevailing soil and climate characteristics within Germany relevant for the different plant development periods. Our statistical models capture collinear factors within yield formation. These are, for example, pests and diseases, or the adaptation behaviour of farmers on changing climatic or economic conditions. Due to the normalization, the yield changes are independent of technological levels and can be combined with weather and climate projection without any bias correction. The coarse temporal subdivision of the climatic variables supports robust assessments of climate change projections. To conclude, our models are suitable for the combination of yield assessments with weather and climate projections, because they reproduce yields from out-of-sample years robustly. In general, the separate time series models reproduce best the measured yield changes.
Key words: Statistical crop yield models, climate impacts, winter wheat, silage maize, volatility
In den Anfangsjahren der Ertragsmodellierung waren statistische Modelle zunächst die einzige praktikable Möglichkeit, witterungsbedingte Schwankungen historischer landwirtschaftlicher Erträge zu modellieren (Doll, 1967; Oury, 1965; Shaw, 1964). Statistische Modelle erklären die Volatilität der endogenen Variable Ertrag aus der Volatilität ertragsrelevanter exogener Variablen (z.B. Niederschlag). Innerhalb einer funktionalen Form werden die ertragserklärenden Parameter der Modelle geschätzt. Die exogenen Variablen sind häufig auf klimatische Einflüsse begrenzt (Iizumi et al., 2013; Lobell und Asner, 2003; Roberts et al., 2012; Schlenker und Roberts, 2009). Sie können aber neben den klimatischen auch pedosphärische und ökonomische (Adaption, Faktor- und Produktpreise) Ertragseinflüsse berücksichtigen (Bakker et al., 2005; Reidsma et al., 2007; You et al., 2009).
Mit der Entwicklung moderner Rechentechnik gewannen prozessbasierte Ertragsmodelle an Bedeutung (Nendel et al., 2013; Tannura et al., 2008). Diese Modelle zerlegen die pflanzenphysiologische Ertragsbildung in Teilprozesse. Theoretisch können prozessbasierte Modelle Ertragsvolatilität für ein weites Spektrum von Umweltbedingungen, mit nur geringen Änderungen im Parametersatz, simulieren (Asseng et al., 2013; Palosuo et al., 2011). Bei den Parametern dieser Modelle handelt es sich nicht, wie bei statistischen Modellen, um Schätzungen, sondern um experimentell begründete Setzungen. Räumliche unterschiedliche Erträge werden bei prozessbasierten Modellen also ausschließlich über die Variation der Variablen, aber nicht der Parameter errechnet.
In den letzten Jahren haben statistische Modelle wieder an Bedeutung gewonnen, da sie, im Gegensatz zu prozessbasierten Modellen, schwer modellierbare Faktoren implizit berücksichtigen können. Zu diesen Faktoren gehören u.a. die Wirkungen von Krankheiten und Schädlingen, vorhandener Agrotechnik oder Faktorpreisen, welche (klimaabhängig und klimaunabhängig) die Bestandesführung und die Anpassungsreaktion der Landwirte an den Klimawandel beeinflussen (Lobell und Burke, 2010). Diese von prozessbasierten Modellen nur mit hohem Aufwand zu erfassenden Faktoren können die direkte Klimawirkung auf den Ertrag überlagern (Challinor et al., 2014). Dies kann Fehleinschätzungen begünstigen.
Ziel der vorliegenden Studie war es, statistische Ertragsmodelle für die Abschätzung von Klimafolgen auf die Erträge landwirtschaftlicher Kulturen zu entwickeln und zu testen. Dabei standen die in Deutschland angebauten Kulturen Winterweizen (Triticum aestivum L.) und Silomais (Zea mays L.) im Mittelpunkt. Winterweizen ist die bedeutendste winterannuelle, Silomais die bedeutendste sommerannuelle Kultur Deutschlands (Statistisches Bundesamt, 2013). Zudem repräsentiert der Winterweizen stellvertretend den Klimaeinfluss auf C3-Pflanzen, mit dem Silomais lässt sich der Klimaeinfluss auf C4-Pflanzen ableiten. Die Ergebnisse zeigen und diskutieren wir auf Modellierungsebene der Landkreise und räumlich aggregiert. Aggregationsebenen sind Deutschland, seine Bundesländer und Flusseinzugsgebiete. Sie werden nachfolgend als Nation und Subnation bezeichnet. Zusammen werden Nation (d.h. Deutschland) und Subnationen (d.h. Bundesländer und Flusseinzugsgebiete) als (Sub)Nation(en) angesprochen.
Die räumliche Heterogenität der Witterungs-Ertragseinflüsse innerhalb der (Sub)Nation(en) lässt sich statistisch über verschiedene Methoden der Parameterschätzung berücksichtigen: indirekt, mit räumlich separat geschätzten Zeitreihenmodellen (STSM), oder direkt, mit Paneldatenmodellen (PDM) oder Zufallskoeffizientenmodellen (RCM). Mit den methodisch sehr simplen STSMs werden die Parameter der Landkreismodelle separat und unabhängig voneinander geschätzt (Lobell und Burke, 2010). Durch die separate Schätzung der STSMs wird die räumliche Heterogenität innerhalb der (Sub)Nation(en) erfasst. PDMs hingegen schätzen zeitliche und räumliche Ertragsänderungen direkt über einen (für alle Landkreise geltenden) Parametersatz je (Sub)Nation (You et al., 2009). Individuelle Witterungs-Ertragseinflüsse können von den PDM-Parametern daher nur (sub)national (Bundesländer, Flusseinzugsgebiete, Deutschland) und nicht auf Landkreisebene erfasst werden. RCMs belegen eine Zwischenposition bei der Parameterschätzung. Sie schätzen auf (sub)nationaler Ebene mit landkreisindividuellen Parametern (Reidsma et al., 2007). Dafür benötigen sie allerdings ein methodisch komplexeres Schätzverfahren.
Durch die Trennung von Modellierungsebene (Landkreise) und Betrachtungsebene (Bundesländer, Flusseinzugsgebiete, Deutschland) wird gezielt die Wirkung von Aggregation genutzt (Woodard und Garcia, 2008). Durch Aggregation werden Einflüsse (z.B. Krankheiten und Schädlinge) herausgefiltert, die auf Landkreisebene die Modelle verzerren. Durch das Filtern kann sich auf den aggregierten Ebenen eine höhere Modellgüte als auf der eigentlichen Modellierungsebene ergeben. Dennoch können über diesen Ansatz landkreisindividuelle Klimaeinflüsse auf den Ertrag erfasst werden (Butler und Huybers, 2013).
Ein Vorzug statistischer Modelle besteht darin, dass sie sich im Unterschied zu prozessbasierten Modellen von den zugrundeliegenden absoluten Niveaus lösen können. Es werden dann nicht mehr die absoluten Erträge, sondern absolute oder relative Änderungen gegenüber dem Vorjahr (erste Differenzen, Quotienten) errechnet. Dies hat sowohl für die Schätzung, als auch für die Anwendung der Modelle Vorteile und Nachteile. Im Vorfeld der Schätzung können durch die Bildung von Differenzen oder Quotienten Ertragstrendeinflüsse oder Änderungen des Trends, durch züchterischen und technologischen Fortschritt, eliminiert werden (Lobell und Asner, 2003; You et al., 2009). Beispielsweise ist durch die Niveaunormierung die Stagnation des Ertragstrends in Deutschland, wie von Brisson et al. (2010) gezeigt, unproblematisch für die Schätzung in statistischen Modellen. Aber auch systematische Fehler der Variablen verlieren an Bedeutung. Eine explizite Fehlermodellierung bei der Verwendung von Daten aus Klimamodellen wird überflüssig. Selbst wenn die Klimamodelle einen systematischen Fehler aufweisen, kann der Ertragseinfluss von Klimaänderungen abgeschätzt werden (Lobell, 2013). Nachteilhaft ist, dass durch die Trennung vom absoluten Niveau nur noch begrenzt Aussagen über dessen Veränderung gemacht werden können (da dieses nicht mehr in den Daten und Parametern enthalten ist). Zudem wird bei der Schätzung nicht mehr die Niveauabhängigkeit in den Relationen zwischen Ertrag und Ertragsfaktoren berücksichtigt.
Für die von uns geprüften Modellansätze verwendeten wir, analog zu Oury (1965), die Cobb-Douglas-Produktionsfunktion als funktionale Form. In dieser wurden von uns logarithmierte erste Differenzen zueinander in Beziehung gesetzt. Die logarithmierten ersten Differenzen der Erträge bzw. der ertragsbeeinflussenden Faktoren werden nachfolgend vereinfachend als relative Ertrags- bzw. Faktoränderung bezeichnet. Die Cobb-Douglas-Produktionsfunktion berücksichtigt Substitution und Interaktion zwischen den exogenen Variablen. Zudem sind die Parameter als relative Ertragsänderungen zu interpretieren und daher direkt miteinander vergleichbar (Wooldridge, 2013: 351–354). Eine Vielzahl anderer funktionaler Formen ist möglich. Wir beschränken uns auf die Cobb-Douglas-Produktionsfunktion, da sie sich sowohl in ökonomischen (You et al., 2009) als auch pflanzenbaulichen Anwendungen (Lee et al., 2013) bewährt hat.
Da das Klima in den phänologischen Entwicklungsphasen unterschiedlich auf den Ertrag wirkt (Chmielewski et al., 2004), ist eine zeitliche Aufteilung der Wachstumsperiode sinnvoll. Dixon et al. (1994) und Lobell et al. (2011) teilen die Klimavariablen phänologisch nach Kalendermonaten ein. Chmielewski und Köhn (2000) verwenden für ihre Ertragskomponentenanalyse von Winterroggen fünf phänologische Entwicklungsperioden unabhängig von den Kalendermonaten. Moore und Lobell (2014), Butler und Huybers (2013) und You et al. (2009) unterteilen die Wachstumsperiode nicht. Wir nutzten eine vergleichsweise grobe Unterteilung nach Viertel- und Halbjahren, um partielle Klimawirkungen während der vegetativen und generativen Entwicklung abzubilden. Diese grobe Unterteilung erachteten wir als ausreichend für die Anwendung der Modelle zur Abschätzung von Klimafolgen, da Klimasimulationen robuste Tendenzen erst bei gröberer zeitlicher Aggregation erkennen lassen.
Die Einteilung der Klimavariablen basiert auf zwei Haupteinflussfaktoren. Der erste Einflussfaktor ist die durch die Globalstrahlung (Rs) ankommende Energie. Diese bestimmt das potenzielle Wachstum der Pflanze (Monteith, 1977). Faktoren, die dieses potenzielle Wachstum negativ beeinflussen, lassen sich als Stressfaktoren (zweiter Einflussfaktor) beschreiben. Besonders sensitiv reagieren Pflanzen in Deutschland auf eine unzureichende Wasserversorgung (Chmielewski und Köhn, 2000; Kersebaum und Nendel, 2014). Die Wasserversorgung wurde durch die Variablen Niederschlag und potenzielle Evapotranspiration (ETP) abgebildet. Andere Stressfaktoren, wie z.B. hohe Temperaturen (Lobell et al., 2013) werden nicht berücksichtig, da sie vergleichsweise selten in Deutschland wirksam werden.
Zwischen den Klimavariablen in einem statistischen Modell kann Multikollinearität, das heißt eine Korrelation der exogenen Variablen untereinander auftreten. Beispielsweise ist die Rs hoch mit der Temperatur (Bristow und Campbell, 1984) und aus der Temperatur (T) errechneten Variablen korreliert (Lobell, 2010). Dixon et al. (1994) und Lobell und Asner (2003) verwenden die Rs als ertragserklärende Klimavariable. Dixon et al. (1994) zeigen, dass das Weglassen der Rs zwar nur zu einem geringen Verlust an Erklärungskraft führt. Allerdings ändern sich die Parameter beträchtlich (omitted-variable bias) und die Modelle verlieren deutlich an Voraussagefähigkeit (gemessen am RMSE). Als Proxyvariable für Rs verwenden You et al. (2009) den Bewölkungsgrad. Wir verwendeten eine temperaturnormierte Globalstrahlung (SRT), um einerseits den Strahlungseinfluss auf den Ertrag abzubilden und andererseits Kollinearität mit temperaturabhängigen Variablen, wie Sättigungsdefizit (VPD) oder ETP zu mindern.
Kaufmann und Snell (1997) diskutieren, dass nicht im Modell berücksichtigte, aber ertragsrelevante (ökonomische) Variablen zu einem omitted-variable bias führen. Ertragseffekte durch sich ändernde ökonomische Bedingungen können die Ertragswirkungen der interannuellen Klimaänderungen überlagern (Reidsma et al., 2007). Gerade auf weniger produktiven Ertragsstandorten haben sich die Anbaufläche und die Intensität des Faktoreinsatzes durch gesetzliche Flächenstilllegungsquoten und über die Förderung von Biogas und Biodiesel geändert (Krause, 2008). Aus diesem Grund sind konstante Bewirtschaftungsbedingungen über den betrachtenden Zeitraum und innerhalb von Deutschland nicht realistisch (vgl. Lobell und Asner, 2003). Um die ökonomischen Ertragswirkungen abzubilden, nutzten wir als ökonomische Proxyvariablen Düngerpreis und Anbaufläche der jeweiligen Kultur. Der Düngerpreis bildet den Produktionsfaktoreinsatz bei sich ändernder Rentabilität ab. Die im Zeitraum 1991 bis 2010 gestiegene Anbaufläche von Winterweizen (+34%) und Silomais (+40%) steht für die Änderung der Gemeinsamen Agrarpolitik (GAP).
Wir prüften die Leistungsfähigkeit des oben skizzierten Konzeptes zur niveauneutralen Ertragsmodellierung auf eine Anschlussnutzung in der Klimafolgenforschung. Es wurde gezielt die Wirkung von Aggregation genutzt. Die Parameterschätzung wurde auf Landkreisebene vorgenommen, die Modellevaluierung erfolgte auf (sub)nationaler Ebene (Bundesland, Flussgebiet und Deutschland). Die Vor- und Nachteile von drei statistischen Ansätzen (STSMs, PDMs, RCMs) wurden dargestellt und diskutiert.
Die Ertragsdaten wurden landwirtschaftlichen Ertragsstatistiken der deutschen Landkreise von 1991 bis 2010 entnommen. Die klimatischen Einflüsse auf den Winterweizen- und Silomaisertrag wurden über die Klimavariablen ETP, SRT und Niederschlag (Nied) abgebildet (Tab. 1). Die Klimavariablen wurden aus den Daten der einzelnen, über Deutschland verteilten, Wetterstationen berechnet. Aus den täglichen Stationsdaten wurden zunächst die genannten Variablen berechnet, dann wurden diese zu Halb- und Vierteljahreswerten summiert und schließlich für jeden Landkreis gemittelt. Die ökonomischen Proxyvariablen Anbaufläche der jeweiligen Kultur und Düngerpreis liegen nur für Gesamtdeutschland vor. Sie flossen deshalb nicht landkreisindividuell in die Modelle ein. Eine ausführlichere Beschreibung der Datenbasis befindet sich im Appendix A.1.
Tab. 1. Genutzte exogene Variablen für das Winterweizen- (WW) und das Silomaismodell (SM). Die Variablen unterscheiden sich hinsichtlich ihrer zeitlichen Einteilung (Periode), der Aggregation und nach der räumliche Beobachtungsebene (Ebene mit LK = Landkreis und Nat = National). Die Perioden stehen für die Kalendermonate November bis April (Nov–Apr), Mai bis Juli (Mai–Juli) und August bis Oktober (Aug–Okt). Die abgekürzten exogenen Variablen sind potenzielle Evapotranspiration (ETP), temperaturnormierte Globalstrahlung (SRT). Das Basisjahr des Indexes ist 2005 = 100
Variable | Kultur | Periode | Aggregation | Ebene |
ETP | WW | Nov–Apr | Summe | LK |
ETP | WW, SM | Mai–Juli | Summe | LK |
ETP | SM | Aug–Okt | Summe | LK |
Niederschlag | WW | Nov–Apr | Summe | LK |
Niederschlag | WW, SM | Mai–Juli | Summe | LK |
Niederschlag | SM | Aug–Okt | Summe | LK |
SRT | WW, SM | Mai–Juli | Summe | LK |
Düngerpreis | WW, SM | Jan–Dez | Index | Nat |
Ackerfläche WW | WW | Jan–Dez | Index | Nat |
Ackerfläche SM | SM | Jan–Dez | Index | Nat |
Die tägliche SRT wird nach Gleichung 1 berechnet. Um eine Division durch Null zu vermeiden, wurde die Temperaturachse um den Summanden 20 korrigiert (vgl. Oury, 1965, Ariditätsindex nach de Martonne).
RS |
– |
tägliche Globalstrahlung [J cm–2], |
Tavg |
– |
durchschnittliche Tagestemperatur [°C], |
SRT |
– |
temperaturnormierte Globalstrahlung |
Die ETP (Gleichung 2), berechnet nach Haude, setzt sich aus zwei Teilen zusammen: dem Haude-Faktor fH und dem VPD (Bormann und Richter, 1996; Schrödter, 1985). Da die fH für Mais und Weizen nicht für die gesamte Wachstumsphase dieser Kulturen verfügbar sind, verwendeten wir für fH das arithmetische Mittel der fH-Werte von Weizen, Mais und Grünland. Diese berücksichtigen die spezifischen Eigenschaften von Weizen und Mais und sind monatsweise für das ganze Jahr verfügbar.
fH |
– |
Haude Faktor, |
VDP |
– |
tägliches Sättigungsdefizit [hPa]. |
Das VPD (Gleichung 3) errechnet sich nach der Magnus-Formel aus Maximumtemperatur (Tmax) und Taupunkttemperatur (DVWK, 1996; Sonntag, 1990). Näherungsweise kann statt der Taupunkttemperatur die tägliche Minimumtemperatur (Tmin) verwendet werden (Castellvi et al., 1996; Roberts et al., 2012). Den von Roberts et al. (2012) und Donatelli et al. (2006) genutzten Skalierungsfaktor ersetzten wir durch den Faktor der Magnus-Formel (6.11) nach Sonntag (1990).
Die zeitliche Aggregation unserer Klimavariablen orientierte sich an der phänologischen Entwicklung von Winterweizen und Silomais in Deutschland. Die Aussaat- und Erntezeiten von Winterweizen und Silomais variieren zwischen den Jahren und den Landkreisen. Von 1992–2010 erfolgt die Aussaat von Winterweizen näherungsweise von Anfang bis Mitte Oktober (± 4 Tage) (Auflaufen Ende Oktober) und jene von Silomais gegen Ende April (± 5 Tage) (Auflaufen Anfang Mai). Die Erntezeit von Winterweizen ist näherungsweise Anfang August (± 12 Tage) und von Silomais Ende September (± ein Monat). Innerhalb von Deutschland variiert die Erntezeit von Weizen um ± einen Monat, von Silomais um ± 22 Tage (DWD, 2014). Für die Ertragsmodelle verwendeten wir Viertel- und Halbjahressummen der Klimavariablen ETP, SRT und Nied. Diese charakterisieren die klimatischen Bedingungen während der vegetativen und generativen Wachstumsphasen der betrachteten Kulturen in Deutschland. In unseren Modellen erstreckte sich die vegetative Phase des Winterweizens vom November des Aussaatjahres bis zum April des Erntejahres, bei Silomais ging sie vom Mai bis zum Juli des Erntejahres. Die generative Phase umfasst die Monate Mai bis Juli beim Winterweizen und August bis Oktober beim Silomais (wir nahmen den auf volle Monate gerundeten spätesten Erntezeitpunkt).
Als Grundmodell wurde die Cobb-Douglas Produktionsfunktion verwendet (Gleichung 4). Mit der Funktion werden die relativen Ertragsänderungen (Änderungen im Vergleich zum Vorjahr) durch die relativen Änderungen der exogenen Variablen geschätzt.
|
|
– |
relative Ertragsänderungen im Jahr t in Relation zum Jahr t – 1 (endogene Variable), |
|
|
– |
relative Änderungen klimatischer (j) und ökonomischer (k) Ertragsfaktoren im Vergleich zum Vorjahr (exogene Variablen), |
|
– |
Parameterwert für den mittleren Trendeinfluss, |
|
– |
Parameter für den Faktoreinfluss der j-ten klimatischen und k-ten ökonomischen Variable. Die Parameter beschreiben den relativen Effekt auf den Ertrag (in Prozent) beim Anstieg einer klimatischen oder ökonomischen Variable um ein Prozent. |
Das Grundmodell wurde mit drei unterschiedlichen Regressionsmethoden geschätzt. Die Methoden unterschieden sich hinsichtlich ihrer Berücksichtigung von landkreisindividuellen Ertragseinwirkungen. Zur Vergleichbarkeit der Methoden waren funktionale Form und Transformation für alle Modelle einheitlich. Um die Cobb-Douglas Produktionsfunktion zu linearisieren, wurde das Grundmodell (Gleichung 4) logarithmiert. Durch die Transformation der Modellterme wurden diese für Regressionsmodelle nutzbar: log((xt/xt–1)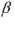
) = 
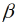log (xt/xt–1) = 
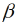(log xt – log xt–1), der transformierte Modellterm log xt – log xt–1 wird nachfolgend als Δ log xt bezeichnet. Zudem wurde das Grundmodell um den Fehler u erweitert.
Das STSM (Gleichung 5) schätzt relative Ertragsänderungen der einzelnen Landkreise, i = 1, …, N, unabhängig voneinander (Dielman, 1983). Durch die separate Schätzung von N Modellen wird im Nachhinein die räumliche Heterogenität berücksichtigt. Der Landkreisindex i ist bei der Schätzung der einzelnen Zeitreihenmodelle noch nicht relevant, sondern hat erst bei der Betrachtung aller separaten Modelle einer (Sub)Nation Bedeutung.
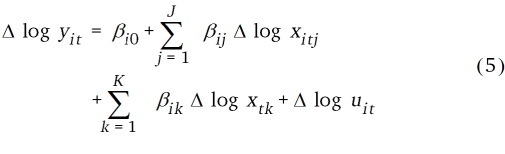
Im Unterschied zu den STSMs schätzen PDMs (Gleichung 6) direkt die Parameter β über alle Landkreise. Die zeitliche und räumliche Volatilität der Variablen wird als unabhängig voneinander angesehen. Im Fehlerterm schätzen die PDMs landkreisindividuelle, zeitinvariante Einflüsse (z.B. Bodenproduktivität) mit dem unbeobachteten individuellen Fehler (Croissant und Millo, 2008; Wooldridge, 2013).
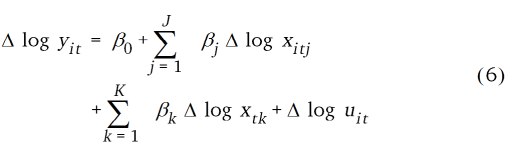
RCMs (Gleichung 7) können zwischen STSMs und PDMs eingeordnet werden. In RCMs werden mittlere (
0, 
j, 
k) und landkreisindividuelle Parameter (bi0, bij, bik) errechnet. Zusammen ergeben beide Parameter (
+ bi) den landkreisindividuellen Ertragseffekt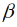 
i. Die Parameter der RCMs können nicht, wie STSMs und PDMs, nach der Methode der kleinsten Quadrate (OLS) geschätzt werden, da die Parameter 
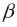j und bij nicht unabhängig voneinander sind. Die RCM-Parameter werden daher mit der Restricted Maximum Likelihood (REML) Methode geschätzt (Reidsma et al., 2007).
Die mit den verschiedenen Modellen modellierten Landkreiserträge wurden (über das arithmetische Mittel) zu (sub)nationalen Erträgen aggregiert (Gleichung 8) und mit den aggregierten Beobachtungen verglichen.
Wir nutzten eine Kreuzvalidierung, um die Vorhersagefähigkeit der Modelle zu testen. Dazu nahmen wir jeweils alle Beobachtungen eines Jahres aus dem Datensatz heraus, schätzten das Modell und simulierten dann den Ertrag für das fehlende Jahr. Die Reproduzierbarkeit des jeweiligen Jahresertrages wurde für den aggregierten Ertrag, d.h. auf der Ebene der (Sub)Nation(en) beurteilt. Diese out-of-sample Prognose führten wir sequentiell für alle Jahre durch.
Die Modelle sollen das mittlere Niveau und die Volatilität der beobachteten relativen Ertragsänderungen reproduzieren. Als Gütemaße verwendeten wir dafür den Root-Mean-Square Error (RMSE), das Bestimmtheitsmaß (R2), das korrigierte Bestimmtheitsmaß (Adj. R2) und den Nash-Sutcliffe Modell-Effizienz-Koeffizienten (NSE). Der RMSE gibt die absolute, mittlere Fehlschätzung an und berücksichtigt daher unterschiedlich langen Zeitreihen. Die Gütemaße R2 und Adj. R2 geben Auskunft wie gut die relative Volatilität der relativen Ertragsänderungen reproduziert wird. Sie zeigen keine Fehlschätzungen des Niveaus an. Das R2 errechnet sich aus den quadrierten Korrelationskoeffizienten zwischen gemessenen und geschätzten relativen Ertragsänderungen für die Ebene der (Sub)Nation(en). Das Adj. R2 berücksichtigt zusätzlich die Anzahl der in das Modell aufgenommenen Variablen. Zur Vergleichbarkeit von PDMs und STSMs verwendeten wir für die Berechnung des Adj. R2 die kritischeren Freiheitsgrade der STSMs. Der NSE reagiert sowohl auf Fehlschätzungen des Niveaus als auch der Schwankungen. Daher ist der NSE auch bei nicht OLS-Bedingungen oder für nicht in die Schätzung einfließende relative Ertragsänderungen (Validierungsergebnisse) nutzbar. Die von Krause et al. (2005) angeführte Überschätzung des NSE bei Extremwerten ist durch die logarithmierten Erträge unproblematisch.
Für STSMs und PDMs testeten wir statistisch die Zulässigkeit von OLS-Schätzern. Die nachfolgenden statistischen Tests werden von Croissant und Millo (2008) und Wooldridge (2013) näher beschrieben. Die funktionale Form prüften wir mit dem Regression Equation Specification Error Test (RESET). Mit dem Lagrange-Multiplier-Test nach Breusch-Pagan (LM) prüften wir die Modelle auf räumliche Heterogenität. Bei Autokorrelation (Breusch-Godfrey-Test) und/oder Heteroskedastizität (Breusch-Pagan-Test) sind die Signifikanztests (t-Test für Parameter) ungültig. Die Standardfehler der Parameter wurden dann durch robuste Standardfehler nach Arellano ersetzt. Normalverteilung der Residuen testeten wir mit dem Shapiro-Wilk-Test.
Zu den RCMs nach REML werden über die genutzten R-Pakete standardmäßig keine statistischen Tests angeboten (siehe Appendix A.2 für eine detaillierte Beschreibung der verwendeten Software). Bei der Schätzung der RCM nach Maximum Likelihood werden das Akaike Information Criterion (AIC) und das Bayesian Information Criterion (BIC) als Gütemaße errechnet. AIC und BIC sind vergleichbar mit dem R2 und dem Adj. R2 bei OLS-Schätzern. Letztere sind aber bei REML (hierarchischen Daten) als Gütemaße problematisch in der Anwendung, da bei diesem Schätzverfahren nicht zwangsläufig (wie bei OLS) das mittlere Niveau getroffen wird. Der NSE kann hingegen bei REML verwendet werden. Der NSE hat zudem den Vorteil, dass er als relatives Maß direkt interpretierbar ist. Die vom BIC vorgenommene Diskriminierung bei zunehmender Variablenanzahl ist für unsere Modelle ohne Bedeutung, da alle Modelle die gleichen Variablen nutzen (Reidsma et al., 2007; Wooldridge, 2013).
Die mit den STSMs, PDMs und RCMs simulierten relativen Ertragsänderungen der Landkreise konnten die mittlere Volatilität der beobachteten Weizenerträge reproduzieren. Es gab jedoch Unterschiede zwischen den Modellen bei der Simulation von außergewöhnlich großen Ertragsschwankungen. Dies wird exemplarisch für den Landkreis Oder-Spree (Brandenburg) in Abb. 1 verdeutlicht. Von den STSMs wurden überdurchschnittlich große relative Ertragsänderungen am besten reproduziert. PDMs zeigten hingegen deutliche Schwächen bei der Reproduktion außergewöhnlich großer und nur regional auftretender relativer Ertragsänderungen (im restlichen Brandenburg ist diese außergewöhnliche relative Ertragsschwankung nicht aufgetreten). Die RCMs lagen zwischen den STSMs und den PDMs (NSEs für den Landkreis Oder-Spree; STSM: 0.68, PDM: 0.21, RCM: 0.66, für Brandenburg: STSM: 0.84, RCM: 0.81, PDM: 0.70).
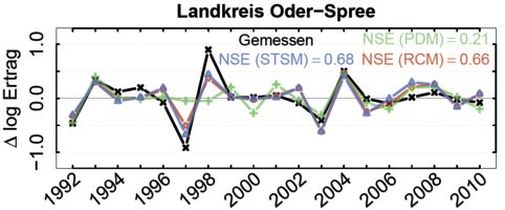
Abb. 1. Gemessene (schwarz) und mit den Modellen STMS, PDM, RCM (blau, grün, rot) geschätzte relative Ertragsänderungen von Winterweizen (Δ log Ertrag) für den Landkreis Oder-Spree (Brandenburg).
Die relativen Ertragsänderungen und Gütemaße für die zu (Sub)Nation(en) aggregierten Modelle sind für STSMs und PDMs exemplarisch in Abb. 2 dargestellt. Die (sub)nationalen relativen Ertragsänderungen der Simulationen und der Kreuzvalidierung wurden nicht systematisch über- oder unterschätzt, da die relativen Ertragsänderungen aus der Kreuzvalidierung sowohl über als auch unter den gemessenen relativen Ertragsänderungen lagen. Die relativen Ertragsänderungen aus der Kreuzvalidierung reagierten nicht sensitiv auf die sich jährlich ändernden Beobachtungen. In den östlichen Regionen erklärten die Simulationen die beobachteten relativen Ertragsänderungen besser als in den westlichen Regionen. Mit steigender Volatilität (hier angegeben als Standardabweichung (SD)) der gemessenen relativen Ertragsänderungen nahm die Erklärungskraft der Modelle je Fruchtart (NSE, R2, Adj. R2 und RMSE) in den Simulationen zu. Für beide Kulturen und alle drei Modellansätze galt, dass die Modelle der kontinentalen, nordöstlichen Subnationen (Brandenburg, Mecklenburg-Vorpommern, Elbe, Warnow/Peene) die höchste Erklärungskraft aufweisen (vgl. auch Tab. 2). Hier besteht bei den gemessenen relativen Ertragsänderungen die höchste Volatilität je Fruchtart. In maritimen (nördlichen) oder bergigen (südlichen) Regionen erklärten die Modelle über die Klimavariablen weniger Volatilität als in kontinentalen Regionen. Trotz der deutlichen Unterschiede in der gemessenen Ertragsvolatilität zwischen Winterweizen (WW) und Silomais (SM) in Ostdeutschland (SD: Brandenburg WW: 0.058, SM: 0.082, Mecklenburg-Vorpommern WW: 0.035, SM: 0.056) bestanden zwischen den Kulturen keine Unterschiede in der Erklärungskraft ihrer Modelle (STSM NSE Brandenburg WW: 0.94, SM: 0.94, Mecklenburg-Vorpommern WW: 0.95, SM: 0.93).
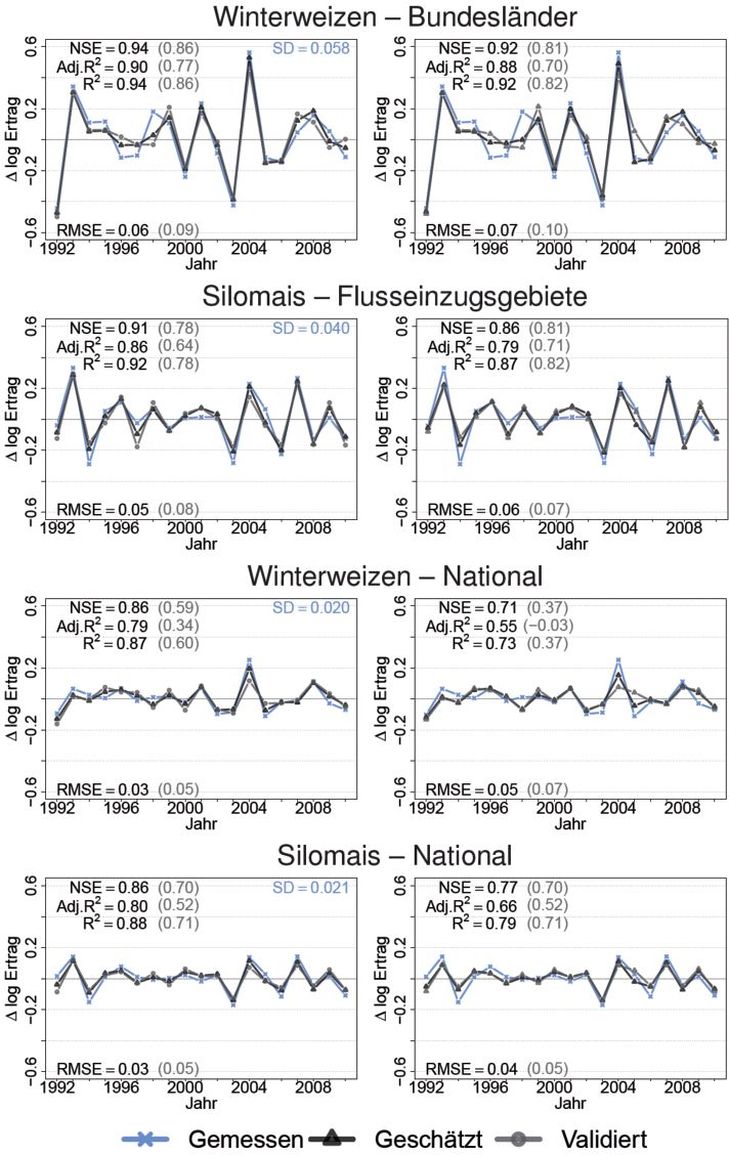
Abb. 2. Gemessene sowie mit zwei Modellen (aggregierte STMS links, PDM rechts) geschätzte und kreuzvalidierte relativeErtragsänderungen (logarithmiert, erste Differenzen) für Winterweizen und Silomais auf verschiedenen regionalen Ebenen. Die relativen Ertragsänderungen sind für Winterweizen auf Bundeslandebene, für Silomais auf Flusseinzugsebene und für beide Kulturen auf nationaler Ebene dargestellt. Die schwarzen Erklärungswerte (NSE, Adj. R², R²) beziehen sich auf die geschätzten Modellergebnisse, die grauen auf die Ergebnisse der Kreuzvalidierung. Die Standardfehler (SD) der gemessenen relativen Ertragsänderungen sind in blau angegeben.
Tab. 2. Nash-Sutcliffe Modell-Effizienz-Koeffizienten (NSE) für den Zusammenhang zwischen den gemessenen und simulierten relativen Ertragsänderungen für die Aggregationsebene Bundesländer, Flusseinzugsgebiete und Deutschland. Die Spalten unterscheiden nach Kulturen (Winterweizen (WW) und Silomais (SM)) und Modellen (STMS, PDM und RCM)
Winterweizen | Silomais | |||||||
(Sub)nation | STSM | PDM | RCM |
| STSM | PDM | RCM | |
Bundesländer (BL) | ||||||||
Schleswig-Holstein | 0.75 | 0.67 | 0.71 | 0.59 | 0.51 | 0.54 | ||
Niedersachsen | 0.89 | 0.82 | 0.86 | 0.78 | 0.65 | 0.72 | ||
Nordrhein-Westfalen | 0.84 | 0.80 | 0.81 | 0.64 | 0.55 | 0.72 | ||
Hessen | 0.64 | 0.59 | 0.60 | 0.69 | 0.60 | 0.65 | ||
Rheinland-Pfalz | 0.70 | 0.64 | 0.68 | 0.62 | 0.57 | 0.60 | ||
Baden-Württemberg | 0.77 | 0.66 | 0.70 | 0.64 | 0.54 | 0.56 | ||
Bayern | 0.74 | 0.56 | 0.65 | 0.67 | 0.51 | 0.57 | ||
Saarland | 0.70 | 0.68 | 0.69 | 0.77 | 0.76 | 0.77 | ||
Brandenburg | 0.94 | 0.92 | 0.93 | 0.94 | 0.93 | 0.94 | ||
Mecklenburg-Vorpommern | 0.95 | 0.91 | 0.93 | 0.93 | 0.90 | 0.92 | ||
Sachsen | 0.85 | 0.72 | 0.79 | 0.73 | 0.58 | 0.72 | ||
Sachsen-Anhalt | 0.90 | 0.87 | 0.89 | 0.93 | 0.92 | 0.93 | ||
Thüringen | 0.66 | 0.61 | 0.63 | 0.81 | 0.78 | 0.79 | ||
Flusseinzugsgebiete (FEG) | ||||||||
Eider | 0.78 | – | – | 0.24 | – | – | ||
Schlei/Trave | 0.74 | 0.65 | 0.72 | 0.56 | 0.52 | 0.53 | ||
Elbe | 0.92 | 0.81 | 0.88 | 0.91 | 0.86 | 0.88 | ||
Weser | 0.87 | 0.82 | 0.84 | 0.84 | 0.77 | 0.82 | ||
Ems | 0.85 | 0.78 | 0.83 | 0.58 | 0.33 | 0.45 | ||
Rhein | 0.78 | 0.69 | 0.74 | 0.77 | 0.68 | 0.73 | ||
Maas | 0.70 | 0.67 | 0.68 | 0.76 | 0.74 | 0.75 | ||
Donau | 0.72 | 0.63 | 0.66 | 0.50 | 0.35 | 0.39 | ||
Warnow/Peene | 0.94 | 0.91 | 0.93 | 0.93 | 0.89 | 0.91 | ||
Oder | 0.76 | 0.76 | 0.76 | 0.93 | 0.91 | 0.92 | ||
Subnationale Mittelwerte | ||||||||
Mittel BL | 0.79 | 0.73 | 0.76 | 0.75 | 0.68 | 0.73 | ||
Mittel FEG | 0.81 | 0.75 | 0.78 | 0.70 | 0.67 | 0.71 | ||
National | ||||||||
Deutschland | 0.86 | 0.71 | 0.81 | 0.86 | 0.77 | 0.80 | ||
Einen vergleichenden Überblick über die erreichte Modellgüte und den Aggregationseffekt geben die Tab. 2 und 3. Diese beziehen sich auf die drei Modelltypen und die beiden Kulturen auf den verschiedenen Aggregationsniveaus. Die STSMs hatten durchgehend höhere NSEs als die PDMs und die NSEs waren auch meistens höher als die der RCMs (Tab. 2). Bei kleinen Flusseinzugsgebieten mit wenigen Landkreisen unterschieden sich die NSEs nicht (z.B. Oder bei Winterweizen). Der winterannuelle Winterweizen erreichte höhere NSEs als der sommerannuelle Silomais auf der subnationalen Ebene, auf der nationalen Ebene waren die NSEs nahezu gleich. Die NSEs aller Modelle waren beim Silomais auf Deutschlandebene (STSM: 0.86, PDM: 0.77, RCM: 0.80) höher als das Mittel der Bundesländer (STSM: 0.75, PDM: 0.68, RCM: 0.73). Beim Winterweizen waren die NSEs der STSM und RCM höher, aber die der PDM geringfügig niedriger. Das Flusseinzugsgebiet Eider ist nur ein Landkreis und daher nicht als PDM oder RCM schätzbar.
Tab. 3. Aggregationseffekt der aggregierten (Sub)Nationen gegenüber den Landkreisergebnissen als
ΔNSE, mit ΔNSE = NSE(Sub)Nation – (N–1NSELandkreise (i) ). Die Spalten unterscheiden nach Kulturen
(Winterweizen (WW) und Silomais (SM)) und Modellen (STMS, PDM und RCM)
Winterweizen |
| Silomais |
| |||||
(Sub)nation | STSM | PDM | RCM |
| STSM | PDM | RCM | |
Bundesländer (BL) | ||||||||
Schleswig-Holstein | 0.08 | 0.01 | 0.10 | 0.10 | –0.07 | 0.16 | ||
Niedersachsen | 0.13 | 0.16 | 0.16 | 0.15 | 0.07 | 0.16 | ||
Nordrhein-Westfalen | 0.16 | 0.14 | 0.25 | 0.14 | –0.03 | 0.31 | ||
Hessen | 0.07 | –0.07 | 0.14 | 0.25 | 0.02 | 0.28 | ||
Rheinland-Pfalz | 0.08 | –0.02 | 0.12 | 0.12 | –0.01 | 0.17 | ||
Baden-Württemberg | 0.11 | 0.00 | 0.11 | 0.09 | –0.04 | 0.14 | ||
Bayern | 0.16 | –0.10 | 0.16 | 0.14 | –0.07 | 0.11 | ||
Saarland | 0.07 | 0.02 | 0.09 | 0.05 | 0.18 | 0.05 | ||
Brandenburg | 0.09 | 0.26 | 0.12 | 0.08 | 0.35 | 0.08 | ||
Mecklenburg-Vorpommern | 0.13 | 0.25 | 0.16 | 0.12 | 0.32 | 0.14 | ||
Sachsen | 0.09 | 0.06 | 0.05 | 0.13 | 0.00 | 0.07 | ||
Sachsen-Anhalt | 0.05 | 0.21 | 0.06 | 0.11 | 0.34 | 0.08 | ||
Thüringen | 0.10 | –0.05 | 0.18 | 0.15 | 0.20 | 0.17 | ||
Flusseinzugsgebiete (FEG) | ||||||||
Eider | 0.00 | – | – | 0.00 | – | – | ||
Schlei/Trave | 0.05 | 0.08 | 0.06 | 0.08 | 0.17 | 0.13 | ||
Elbe | 0.19 | 0.44 | 0.18 | 0.20 | 0.39 | 0.14 | ||
Weser | 0.15 | 0.29 | 0.19 | 0.21 | 0.44 | 0.21 | ||
Ems | 0.12 | 0.23 | 0.16 | 0.06 | 0.19 | 0.02 | ||
Rhein | 0.14 | 0.37 | 0.20 | 0.21 | 0.50 | 0.31 | ||
Maas | 0.03 | 0.14 | 0.05 | 0.19 | 0.33 | 0.23 | ||
Donau | 0.18 | 0.45 | 0.18 | 0.04 | 0.17 | 0.08 | ||
Warnow/Peene | 0.11 | 0.28 | 0.11 | 0.12 | 0.22 | 0.11 | ||
Oder | 0.02 | 0.05 | 0.04 | 0.02 | 0.06 | 0.03 | ||
Subnationale Mittelwerte | ||||||||
Mittel BL | 0.10 | 0.07 | 0.13 | 0.13 | 0.10 | 0.15 | ||
Mittel FEG | 0.10 | 0.26 | 0.13 | 0.11 | 0.27 | 0.14 | ||
National | ||||||||
Deutschland | 0.20 | 0.47 | 0.18 | 0.28 | 0.50 | 0.17 | ||
In Tab. 3 wird deutlich, dass der Aggregationseffekt (Δ NSE) bei den PDMs für Flusseinzugsgebiete am größten war (WW: 0.26, SM: 0.27). Bei den STSMs und den RCMs war er annähernd gleich (0.10–0.15). Der Aggregationseffekt war auf nationaler Ebene am größten (0.30), gefolgt von den Flusseinzugsgebieten (0.17). Der geringste Aggregationseffekt ergab sich bei den Bundesländern (0.11).
Die räumliche Ausprägung des Aggregationseffektes wird in Abb. 3 am Beispiel der Winterweizen STSMs mit Bezug auf die Korrelation zwischen simulierten und geschätzten relativen Ertragsänderungen gezeigt. Da die relativen Ertragsänderungen nicht systematisch überschätzt waren (vgl. Abb. 2, Tab. 2), ist eine Darstellung, die sich auf den geläufigeren R2 als Gütemaß bezieht, hinreichend. Subnationen mit geringen R2s der einzelnen STSMs auf Landkreisebene erreichten nach der Aggregation höhere Erklärungswerte. Unter anderem konnten die relativen Ertragsänderungen der südlichen Subnationen nach der Aggregation besser reproduziert werden. Beispielsweise stieg in der Subnation Bayern das R2 der STSMs von durchschnittlich 0.58 auf 0.74 nach der Aggregation.
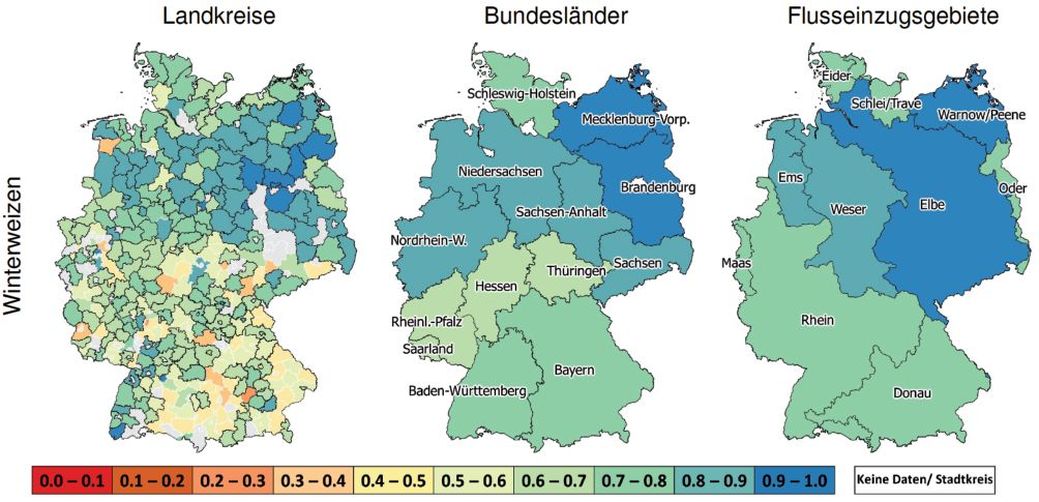
Abb. 3. Räumliche Verteilung der R2 Werte für den Zusammenhang zwischen gemessenen und mittels STSM geschätzten relativen Ertragsänderungen von Winterweizen auf unterschiedlichen Aggregationsebenen. Die linke Karte zeigt die R2 der einzelnen STSM auf Landkreisebene (N = 289). Auf der mittleren und der rechten Karte sind die R2 der aggregierten STSMs für Bundesländer (N = 13) und Flusseinzugsgebiete (N = 10) dargestellt. Die Landkreise mit signifikanten STSM-Modellen (F-Test, p ≤ 0.10) sind auf der linken Karte schwarz umrandet (N = 198).
Die Parameter der STSMs, PDMs und RCMs sind für die beiden Fruchtarten nach Bundesländern (BL) und Flusseinzugsgebieten (FEG) als Boxplots in Abb. 4 dargestellt. Eine große Spannweite der Boxplots bedeutet, dass der Ertragseinfluss des Klimas zwischen den Landkreisen (STSM und RCM) bzw. den Subnationen (PDM) räumlich stark variiert. Generell war die Spannweite der Parameter bei den PDMs und den RCMs deutlich kleiner als bei den STSMs.
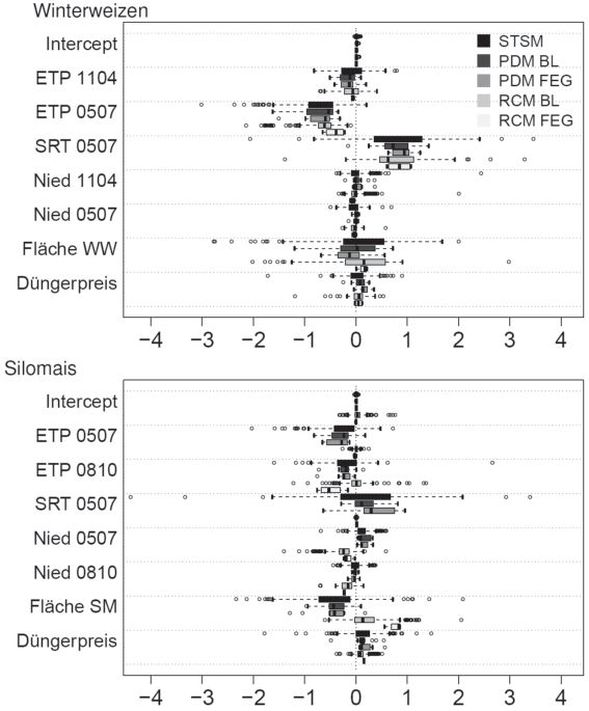
Abb. 4. Geschätzte Koeffizienten der Parameter für alle Modelle für Winterweizen (WW) und Silomais (SM). Die Parameter der STSMs und RCMs beziehen sich auf Landkreise, die Parameter der PDM beziehen sich auf Bundesländer (BL) oder Flusseinzugsgebiete (FEG). Die Zahlen hinter den exogenen Variablen beschreiben die Monate (z.B. 0507 ist Mai bis Juli). Der Balken in der Box ist der Median, die Box repräsentiert das 25% und das 75% Quartil. Die Whiskers sind als Maximum und Minimum definiert, sofern sie kleiner als der 1.5-fache Interquartilsabstand vom Median sind. Ausreißer werden als Punkte dargestellt.
Die räumliche Verteilung für ausgewählte STSM Parameter zeigt exemplarisch Abb. 5. Hier ließen sich klare räumliche Cluster identifizieren. Die Clustergrenzen verliefen intra- und intersubnational, fallen jedoch nur selten mit den Grenzen der Subnationen zusammen. Beim Parameter der ETP zeigte sich in den meisten Landkreisen für beide Kulturen ein deutlich negativer relativer Ertragseinfluss (vgl. auch Abb. 4). Am stärksten (< –1.4%) war dieser Einfluss bei Winterweizen von Mai bis Juli im Bundesland Brandenburg und den angrenzenden Landkreisen (relative Ertragsänderung bei einer relativen ETP Änderung). Für Silomais ergab sich im Erzgebirge (südliches Sachsen) und im Donaueinzugsgebiet ein neutraler bis leicht positiver Ertragseinfluss bei Zunahme der ETP. Niederschlag hatte in der Jugendentwicklung beider Kulturen einen positiven Ertragseinfluss in niederschlagsarmen Regionen, wie Ostdeutschland oder Franken (nördliches Bayern). In Regionen mit mehr Niederschlag hatte dieser einen leicht negativen Einfluss. Das sind in Deutschland der Alpenraum (südliche Grenzen von Deutschland), das Erzgebirge und die Nordseeküste (nördliche Grenze von Niedersachsen, westliche Grenze von Schleswig Holstein). Insgesamt war der relative Ertragseinfluss des Klimas in kontinentalen Regionen größer, als in maritimen oder (den ackerbaulich genutzten Gebieten) in bergigen Regionen.
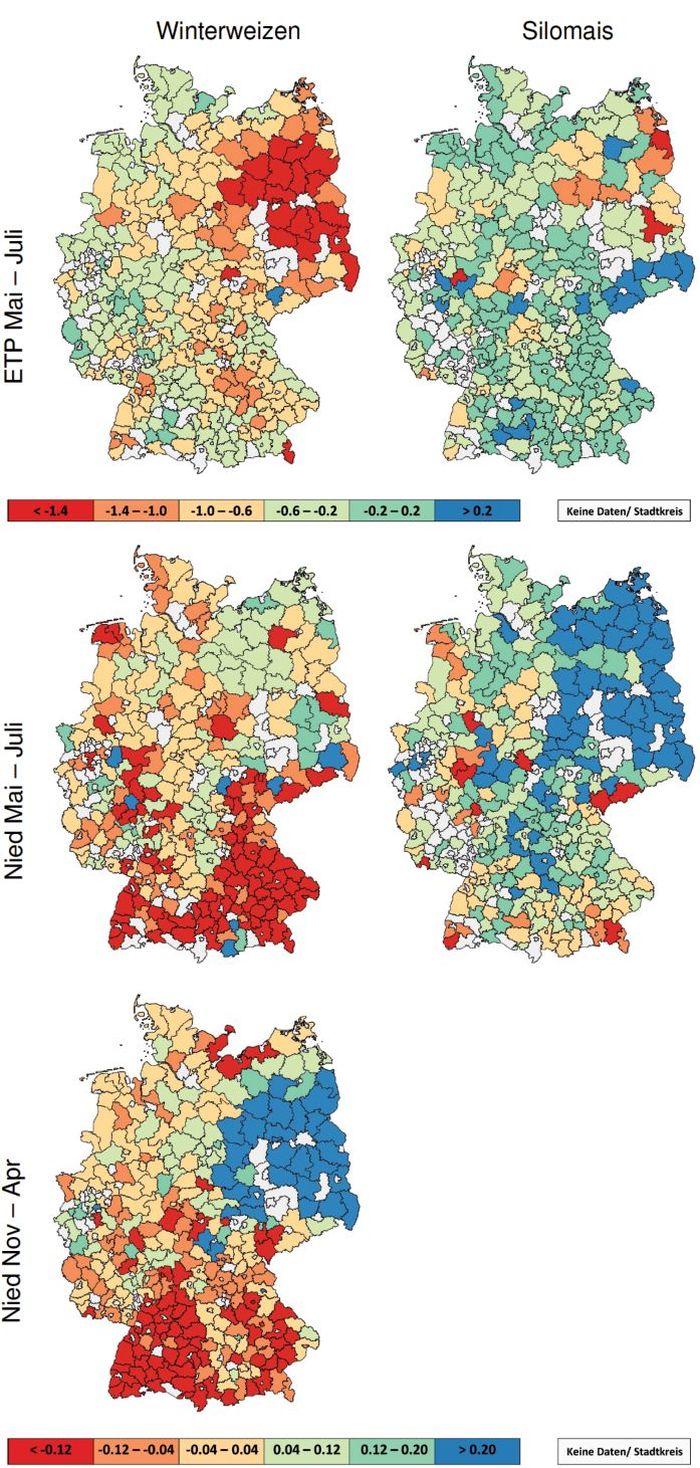
Abb. 5. Räumliche Verteilung der STSM-Parameterkoeffizienten für Winterweizen und Silomais. Die Parameter beschreiben den relativen Ertragseffekt der exogenen Klimavariablen ETP und Nied in den Perioden November bis April und Mai bis Juli.
Die ertragserklärenden klimatischen Variablen zeigten Korrelationskoeffizienten im mittleren Bereich (0.5–0.7), dies deutet auf eventuelle Multikollinearität hin. Die Korrelationskoeffizienten waren teilweise statistisch signifikant (das Signifikanzniveau wird über den p-Wert beschrieben, dabei ist ***: p ≤ 0.01, **: p ≤ 0.05, *: p ≤ 0.1 und ': p > 0.1). Exemplarisch werden nachfolgend Korrelationskoeffizienten der transformierten Klimavariablen von Mai bis Juli aufgeführt. Die SRT war mit der ETP und dem Niederschlag korreliert (0.67***, –0.52***). Die Korrelationen waren statistisch signifikant. Niederschlag und ETP waren ebenfalls signifikant miteinander korreliert (–0.58***). Die Eigenschaften der nicht genutzten RS sind aber dennoch in der SRT enthalten (0.94***). Ein Test auf Multikollinearität der Modelle (Condition Index-Test) ergab jedoch, dass es keine Multikollinearität in den Modellen gab. Düngerpreis und Anbaufläche sind geeignete ökonomische Proxyvariablen, da sie den Faktoreinsatz und die Agrarpolitikänderung abbildeten. Die ökonomische Variable Düngerpreis war stark mit anderen Faktorpreisen, wie dem Saatgutpreis (0.86***) und dem Treibstoffpreis (0.83***), korreliert. Der Brotweizenpreis des Vorjahres (Informationsgrundlage des Landwirts für Faktoreinsatz) war in den 90er Jahren sehr gering mit dem Düngerpreis korreliert (–0.14'), nach der GAP
Reform 2000 (Liberalisierung der Agrarmärkte) jedoch stark mit diesem korreliert (0.81***). Düngerpreis und Anbaufläche von Winterweizen bzw. Silomais waren miteinander stark korreliert (0.72***/0.87***).
Die statistischen Tests geben Aufschluss über die Zulässigkeit der Regressionsmethoden. Für die einzelnen Landkreise, Bundesländer und Flusseinzugsgebiete sind die Ergebnisse der statistischen Tests im Appendix aufgeführt (Abb. A1, Tab. A1). Beim STSM war die genutzte Cobb-Douglas-Funktion als funktionale Form, bis auf wenige Ausnahmen, nicht fehlspezifiziert (RESET). Beim PDM war sie bei Winterweizen teilweise und bei Mais häufig fehlspezifiziert. Weiterhin konnten wir zeigen, dass es in allen Subnationen räumliche Heterogenität gibt (LM-Test) und daher Modelle nötig waren, welche diese berücksichtigen. Autokorrelation und Heteroskedastizität traten bei den STSMs in den überwiegenden Landkreisen nicht auf. Die Modellresiduen waren normalverteilt. Beim PDM sind aufgrund vorliegender Autokorrelation und/oder Heteroskedastizität die Parameter häufig ineffizient. Daher verwendeten wir die robusten Standardfehler nach Arellano. Die Parameter mit den robusten Standardfehlern waren überwiegend signifikant. Die NSEs der RCMs werden zusammen mit den NSEs der STSMs und PDMs in Tab. 2 gezeigt.
Wir zeigten, dass eine niveauneutrale Ertragsmodellierung der klimabedingten Ertragsvolatilität für die beiden wichtigsten landwirtschaftlichen Kulturen Deutschlands möglich ist. Mit allen drei statistischen Modellansätzen ließ sich die zeitliche und räumliche Volatilität der relativen Ertragsänderungen zufriedenstellend reproduzieren und projizieren. Für die Modellierung waren nur wenige, zeitlich grob aufgelöste Klimavariablen notwendig. Die Ergebnisse verdeutlichten jedoch, dass eine zufriedenstellende Modellqualität nicht auf der untersten Modellierungsebene, sondern erst nach einer räumlichen Aggregation auf Bundesländern, Flusseinzugsgebieten bzw. auf nationale Ebene für Deutschland erreicht wurde. Im Unterschied zu prozessbasierten Modellen waren sowohl ertragsbedingte Entscheidungen der Landwirte (Sortenwahl, Beregnung, Wechsel auf marginale Standorte) als auch die Einflüsse von schwer quantifizierbaren Faktoren (Schädlings- und Krankheitsbefall) implizit berücksichtigt. Diese Eigenschaft stellen auch Lobell und Burke (2010) heraus, jedoch berücksichtigen sie keine ökonomischen Variablen wie beispielsweise You et al. (2009), um kollinear verlaufende Effekte aufzufangen.
Die Modelle können unmittelbar genutzt werden, um Ertragseffekte kurz und mittelfristiger Klimasimulationen abzuschätzen. Hierzu sind allerdings im Grundansatz die Parameter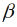 
0 und 
k auf Null zu setzen. In diesen Parametern spiegeln sich der Trendeinfluss und der Einfluss ökonomischer Proxyvariablen wieder. Im Modellansatz wurden sie eingeführt, um den Einfluss der Klimavariablen unverzerrt zu schätzen. Bei den Projektionen spielen sie keine Rolle. Die Projektionen würden das gegenwärtige technologische Niveau stationär fortschreiben. Der CO2-Düngungseffekt würde nicht berücksichtigt werden, könnte jedoch nachträglich durch eine externe Modellierung einbezogen werden. Durch die doppelte Niveauneutralisierung sind die Modelle besonders für die kombinierte Anwendung mit Wetter- und Klimamodellen geeignet. Systematische Fehler in diesen Modellen würden sich nicht auf die Ertragssimulationen auswirken, da diese sich auf Niveauänderungen und nicht auf das Niveau selbst beziehen.
Über die Aggregation wurden höhere Erklärungswerte erreicht. Durch die Aggregation wurden Ausreißer gemildert, indem die Residuen verringert wurden. Diesen Aggregationseffekt finden auch Woodard und Garcia (2008) und Lobell und Burke (2010). Allerdings diskutieren Garcia et al. (1987), dass bei aggregierten Modellierungsebenen regionale Ertragseinflüsse nicht erfasst und damit der Klimaeffekt unterschätzt wird. Da in unseren Modellen aber nur die Aussageebene und nicht die Modellierungsebene selbst aggregiert wurde, sollte dies nicht relevant sein. Garcia et al. (1987) fordern weiterhin die Verwendung von Betriebserträgen. Diese enthalten jedoch viele betriebsindividuelle Einflüsse (Variation in der Bestandesführung) und erhöhen damit die Unsicherheit bei der Parameterschätzung. Auf Landkreisebene heben sie sich in Deutschland wahrscheinlich größtenteils auf. Die Verwendung von Landkreiserträgen sollte daher ausreichend sein für die Abbildung räumlicher Volatilität. Modellabhängig ließ sich ein Aggregationseffekt zeigen, der beim Übergang von den Landkreisen zu(r) (Sub)Nation(en) zu einer Verbesserung der Modellqualität führte. Je höher die Aggregation war desto größer war der Aggregationseffekt, d.h. die Differenz zwischen dem Mittel der Landkreise und der aggregierten ((sub)nationalen) Modellgütemaße.
Die landkreisindividuellen Parameter der STSMs reproduzierten außergewöhnliche, landkreisindividuelle Ertragsschwankungen vergleichsweise gut. Dies war bei Nutzung von PDMs kaum und bei Verwendung von RCMs nur eingeschränkt möglich. Der Vorteil der STSMs gegenüber den PDMs und RCMs erklärt sich aus der Schätzmethode. Während sich die Parameter der PDMs zwischen den Landkreisen nicht unterscheiden und die der RCMs tendenziell weniger variieren, gibt es bei den STSM-Parameter eine stärkere Variation (vgl. Beck und Katz, 2007). PDMs und RCMs besitzen Vorteile, wenn die Datenreihen größere Lücken aufweisen. In diesen Fällen kann es bei den STSMs zu größeren Fehlschätzungen kommen. In Abhängigkeit vom Umfang der Datenlücken, kann dann alternativ auf RCMs und PDMs zurückgegriffen werden.
Für die STSM-Parameter der Klimavariablen zeigten sich deutliche räumliche Cluster. Diese waren nicht deckungsgleich mit den Bundesländern oder Flusseinzugsgebieten. Vielmehr orientierten sie sich an pedosphärischen und topographischen Lagen und spiegelten die Anbaueignung von Winterweizen und Silomais nach Boden- und Klimalagen wieder. Silomais hat als C4-Pflanze eine höhere Strahlungsnutzungseffizienz als Winterweizen (Monteith, 1977). Letzterer reagiert daher sensitiv auf relative SRT-Änderungen. Die räumlichen Cluster der SRT-Parameter ließen sich über ähnliche Cluster absoluten Niveaus der SRT erklären. Chmielewski und Köhn (2000) stellen zu Winterroggen heraus, dass die Sonnenscheindauer gerade nach der Blütephase einen deutlich positiven Effekt auf den Ertrag hat. Dies deckt sich mit unseren Ergebnissen für Winterweizen. Die Erträge von Winterweizen und Silomais reagierten unterschiedlich sensitiv auf eine Änderung der Wasserversorgung. Silomais reagierte im Osten positiv auf Niederschlagszunahmen in den Monaten Mai bis Juli, da hierdurch seine Jugendentwicklung gefördert wird. Im Alpenvorland zeigten die Parameter nur geringe Ertragseffekte. Dies kann über die ausreichende Wasserversorgung erklärt werden. Für den Winterweizen waren relative ETP-Änderungen bedeutender als für Silomais. Von Mai bis Juli ist die Jugendentwicklung des Winterweizens abgeschlossen und dieser befindet sich in der Phase des generativen Wachstums (DWD, 2014). Bei einem ETP-Anstieg kommt es auf den wasserlimitierten Standorten (sandige Böden) schnell zur Limitierung von ertragsrelevanten Prozessen. Für Silomais war der ETP-Ertragseffekt auf stauwassergefährdeten und flachgründigen Böden (Erzgebirge, Donauquellgebiet) leicht positiv. Roberts et al. (2012) stellen für die USA in den Monaten vor der Ernte (Juli–August) einen negativen Ertragseffekt durch das VPD, für die gesamte Wachstumsperiode aber einen positiven Ertragseffekt durch das VPD heraus. Chmielewski und Köhn (2000) zeigen hingegen einen negativen Ertragseffekt für ETP während der Winterruhe und einen positiven Effekt von der Blüte bis zur Ernte. Beide berücksichtigen aber zusätzlich noch die Wachstumsgradtage (Berechnung siehe Appendix A.3) bzw. die Temperatur als Variable, die in beiden Studien einen negativen Ertragseffekt hat. Da wir die Wachstumsgradtage nicht berücksichtigten (wegen der hohen Korrelation (0.91***) mit der ETP) und unsere ETP daher beide Einflüsse abdeckt, waren die Parameter deutlicher negativ. Entsprechend schlussfolgern wir, dass in unseren Parametern der negative Effekt der Wachstumsgradtage enthalten ist. Während der Jugendentwicklung des Winterweizens von November bis April gab es jedoch, analog zum Silomais, einen unmittelbar positiven Effekt von interannuellen Niederschlagsanstiegen auf ertragsbildende Prozesse. Der hohe Niederschlagseffekt im Osten Deutschlands ist auf das geringe absolute Niederschlagsniveau und auf das geringe Wasserspeichervermögen der sandigen Böden in der Region zurückzuführen. Im Alpenvorland wirkte ein Anstieg des Niederschlags negativ. Der negative Niederschlagseinfluss kann auf das hohe Niederschlagsniveau in der Region zurückgeführt werden.
Durch die Cobb-Douglas Produktionsfunktion ist der Ertragseinfluss der Parameter direkt miteinander vergleichbar. Generell zeigten die Niederschlagsparameter bei beiden Kulturen in allen Modellen nur einen sehr geringen Ertragseinfluss. Eine Begründung dafür könnte sein, dass die zu Monaten und Landkreisen aggregierten Niederschlagsvariablen nur begrenzt lokale Niederschlagsextreme oder kurze Trockenperioden erfassen. Da aber auch Trockenjahre wie 2003 von den Modellen abgebildet werden, befinden wir die zeitliche Aggregation der Klimavariablen als ausreichend. Bedeutender als die Aggregation sind die Eigenschaften der Variablen und der Methodik des statistischen Schätzverfahrens. Der Ertragseinfluss einer Klimavariablen findet nicht nur in der absoluten Größe des Parameterwertes (βj) seinen Ausdruck, sondern auch in der Ertragsvolatilität, die durch das Produkt von Parameter und exogener Variable errechnet wird (erklärte Varianz von βj xj). In unserem Datensatz schwankte der Niederschlag um ± 43%. Im Vergleich dazu schwankten ETP und SRT nur um ± 17% und ± 8% (Variablen als log erste Differenzen, Zeitraum Mai bis Juli). Durch die hohe Volatilität der Niederschlagsvariable (relative SD) fielen die Niederschlagsparameter daher klein aus. Für die Bewertung des Ertragseinflusses des Klimas ist aber die erklärte Ertragsvolatilität wichtiger als die Parametergröße. Hier zeigte sich, dass die durch den Niederschlag erklärte Ertragsvariation deutlich größer ist als der Ertragseinfluss der Niederschlagsparameter. Dies könnte auch die von Moore und Lobell (2014) gezeigte geringe Ertragswirkung des Niederschlages erklären, da die Autoren sich bei Ihrer Analyse auf die Parameterwerte beschränken.
Zwischen den exemplarisch getesteten Kulturen Winterweizen und Silomais bestanden auf Deutschlandebene nur geringe Unterschiede in der Modellgüte. Die teilweise höheren Erklärungswerte beim Winterweizen auf Subnationsebene ließen sich im Westen von Deutschland über die Volatilität der Erträge erklären. Im Westen von Deutschland war die Varianz der relativen Ertragsänderungen von Winterweizen größer-gleich der von Silomais. Im Osten von Deutschland war hingegen die Varianz der relativen Silomaisertragsänderungen deutlich größer oder zumindest gleich den relativen Winterweizenertragsänderungen. Die höhere Ertragsvolatilität der Silomaiserträge im Osten zeigen, dass Silomais auf trockenen Standorten deutlich sensitiver auf die Witterung reagiert. Dieser Effekt wird noch verstärkt durch die Ausdehnung des Silomaisanbaus in den letzten Jahren auf marginale, sandige Standorte (Krause, 2008). Auf diesen Standorten können winterannuelle Kulturen ungünstige Wachstumsbedingungen über die Ertragskomponenten eher kompensieren (Chmielewski und Köhn, 2000). Umgekehrt ist bei ausreichender Wasserversorgung die Klimasensitivität von Winterweizen höher und somit Silomais robuster gegenüber der Witterung. Dies konnte gebietsweise im Westen von Deutschland beobachtet werden. Die Bedeutung der Wasserversorgung von Winterweizen in Deutschland wird ebenfalls von Kersebaum und Nendel (2014) herausgestellt.
Die Einteilung der Klimavariablen nach Monaten war eine Annäherung an die zeitlich und räumlich unterschiedlich eintretenden phänologischen Entwicklungsstadien. Dixon et al. (1994) vergleichen die Einteilung der Klimavariablen nach phänologischen Entwicklungsperioden gegenüber Kalendermonaten. Sie zeigen, dass eine räumlich und zeitlich differenzierte Einteilung nach phänologischen Entwicklungsstadien nur geringe Wirkung auf die Erklärungswerte und Voraussagefähigkeiten von statistischen Modellen hat. Zudem ermöglicht unsere grobe Einteilung die Nutzung der Ertragsmodelle in Kombination mit Klimamodellen und gewährleistet eine weitgehende Unabhängigkeit zwischen den Variablen (Multikollinearität).
Da die von uns verwendeten Modelle keine Multikollinearität enthalten, kann ein potenzieller omitted-variable bias vernachlässigt werden. Fehlende ertragsrelevante Variablen bedingen dann lediglich eine geringere Erklärungskraft der Modelle. Lobell et al. (2013) zeigen, dass das VPD und nicht die Temperatur pflanzenphysiologisch auf den Maisertrag in den USA wirkt. Die in dieser Studie genutzte ETP hat gegenüber dem von Roberts et al. (2012) und Lobell et al. (2013) genutzten VPD den Vorteil, dass sie die Pflanzenbedeckung über den Haude-Faktor berücksichtigt. Reidsma et al. (2007) zeigten, dass Modelle ohne ökonomische Variablen den Klimaeffekt überschätzen. Durch die ökonomischen Proxyvariablen war davon auszugehen, dass die Parameter der Klimavariablen unverzerrt sind. Durch die Korrelation der Proxyvariablen untereinander war hier eine Verzerrung der Parameter durch omitted-variable bias nicht ausgeschlossen. In der vorliegenden Studie wurden die Parameter der Proxyvariablen nicht weiter verfolgt, da sie den Ertragseinfluss des Proxys enthalten und daher nicht interpretiert werden können (Wooldridge, 2013: 298–300). Unsere Variablenauswahl war pflanzenphysiologisch und produktionstechnisch begründet. Die sehr hohen Erklärungswerte der Modelle sprechen dafür, dass wir die ertragsrelevanten Einflüsse in unseren Modellen berücksichtigen. Modelle, die eine schrittweise Variablenauswahl nutzen, erfassen eventuell aufgrund mangelnder Signifikanz ertragsrelevante Einflüsse nicht und sind daher verzerrt (siehe Appendix A.4).
Die Variablenauswahl erfolgte einheitlich für alle Landkreise. Teilweise wurden die Parameter nicht signifikant verschieden von Null geschätzt (siehe dazu Appendix A.4). Somit fand über die Parameter eine Korrektur der generellen Variablenauswahl statt. Die NSEs der geschätzten und validierten Erträge zeigten aber, dass, trotz teilweise nicht signifikanter Modelle, nicht durchgehend erfüllter OLS-Bedingungen oder Fehlspezifikation, die Modelle robuste Ergebnisse liefern und für Voraussagen geeignet sind.
Mit den Modellen können Ertragsabschätzungen für die kurz- und mittelfristige Klimazukunft bei unterschiedlicher Datenlage durchgeführt werden. Mit zunehmender Vollständigkeit der Datenreihen nimmt die Eignung der Modelle in der Reihenfolge PDM, RCM und STSM zu. Die Modelle können als Entscheidungshilfe bei Investitionen (z.B. in Beregnungstechnik) oder bei der Bepreisung des Risikos durch Wetterderivate genutzt werden.
Die Winterweizen- und Silomaiserträge liegen auf Landkreisebene für den Zeitraum von 1991 bis 2010 vor. Die Erträge von 1991 bis 1998 sind von uns aus den statistischen Jahrbüchern der deutschen Bundesländer digitalisiert worden. Die Erträge von 1999 bis 2010 sind über Statistische Ämter des Bundes und der Länder (2013b) digital verfügbar. In den Bundesländern Sachsen geht die Zeitreihe insgesamt nur von 1992 bis 2007, in Sachsen-Anhalt von 1991 bis 2006. Landkreise ohne oder mit unvollständigen Ertragsdaten bleiben unberücksichtigt. Der Wetterdatensatz enthält Temperatur als Tages-Maximum (Tmax), -Minimum (Tmin) und -Mittel (Tavg) sowie Globalstrahlung (RS) und Niederschlag als Tagessummen (DWD, 2011). Räumlich wurden die 1218 Wetterstationen des Deutschen Wetterdienstes den Landkreisen zugewiesen. Bei mehreren Wetterstationen in einem Landkreis wurde das arithmetische Mittel genommen. Landkreise ohne Klimastation und Klimastationen oberhalb von 700 m über Normalhöhennull blieben unberücksichtigt. Wir verwendeten diese Höhenrestriktion, da in Deutschland oberhalb davon kein Ackerbau praktiziert wird. Die ökonomischen Proxyvariablen Anbaufläche und Düngerpreis liegen auf Deutschlandebene vor. Die Anbaufläche von Weizen und Silomais wurde aus den Datensätzen von Statistische Ämter des Bundes und der Länder (2013a) [1991 bis 2008] und des „Statistisches Bundesamt“ (2013) [2008 bis 2010] zusammengesetzt. Der Düngerpreisindex und weitere getestete Faktor- und Produktpreise kommen von Statistische Ämter des Bundes und der Länder (2013) und Statistische Ämter des Bundes und der Länder (2013c).
Die Modelle wurden mit der Software R (R Core Team, 2013) geschätzt. Für die PDMs nutzten wir das R-Software-Paket plm (Croissant und Millo, 2008), für die RCM das lme4-Paket (Bates, 2010) und für die statistischen Tests das lmtest-Paket (Zeileis und Hothorn, 2002). Die robusten Standardfehler nach Arellano wurden über das sandwich-Paket errechnet (Zeilleis, 2004). Die Zuweisung der Wetterstationen und die Aggregation zu (Sub)Nationen erfolgten über das sqldf-Paket (Grothendieck, 2012). Die Karten wurden mit dem grafischen Informationssystem Q-GIS erstellt.
Die nachfolgende Formel zeigt die Berechnung der Wachstumsgradtage (WGT) aus TUL mit 8°C und TOL mit 32°C als unsteteres und oberes Limit (Roberts et al., 2012):
Statistisch signifikante Parameter sind nicht alleine für die Variablenauswahl ausschlaggebend (Wooldridge, 2013: 127–129). Nuzzo (2014) zeigt, dass durch den p-Wert Ergebnisse plausibler gemacht werden können. Eine hohe statistische Signifikanz bedeutet aber nur, dass die Wahrscheinlichkeit des richtigen Ergebnisses steigt. Wooldridge (2013: 141) beschreibt, dass einzeln statistisch signifikante Variablen in der Kombination mit anderen Variablen nicht mehr signifikant sind und vice versa. Nach Studenmund (2000: 172–173) ist eine schrittweise Regression, die nacheinander signifikante Variablen in ein Modell aufnimmt, ein Eingeständnis von Unwissenheit über die Variablenauswahl. Wegen der willkürlichen Reihenfolge mit der die Auswahl erfolgt, gibt es keine theoretische (kausale) Begründung für die Variablenauswahl.
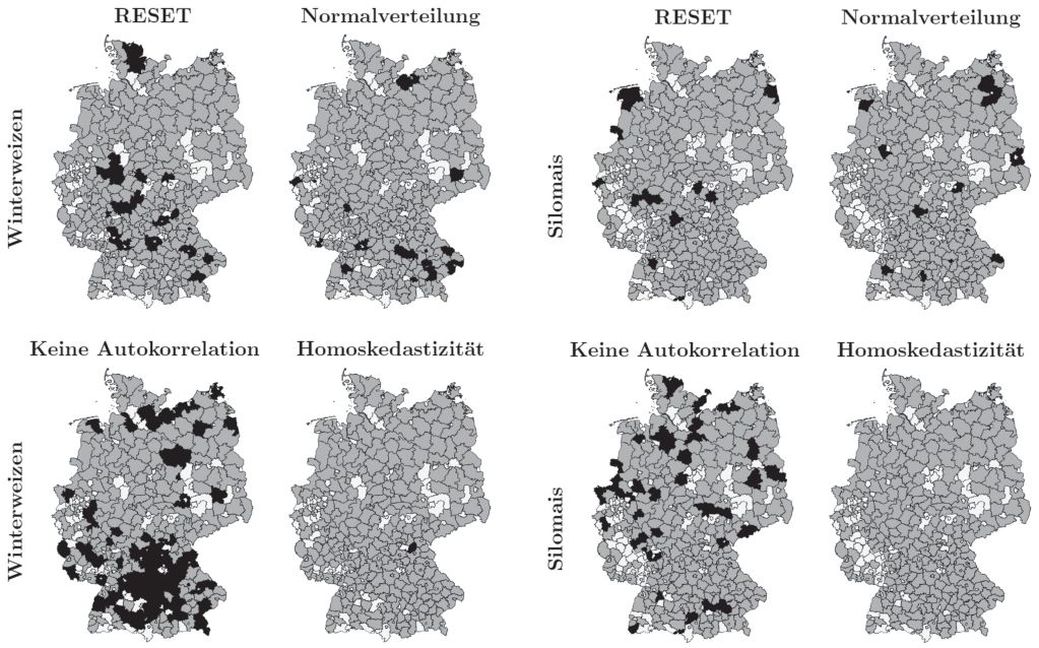
Abb. A1. Statistische Tests der STSMs für Winterweizen und Silomais: Funktionale Form (RESET): Nicht Fehlspezifiziert 
, Normalverteilt (Shapiro-Wilk-Test): , Keine Autokorrelation (Breusch-Godfrey/Wooldridge-Test): , Homoskedastisch (Breusch-Pagan-Test): .
Tab. A1. Statistische Tests der PDMs: Die statistischen Test sind binär dargestellt p ≤ 0.01 → 1, p > 0.01 → 0. FF: RESET (funktionale Form), 1 = Fehlspezifiziert, quadratische Terme haben einen Effekt; HT: Hausman-Test, 1 = fixed effect Transformation besser als random effects Transformation; LM: Lagrange-Multiplier-Test, 1 = signifikante Differenzen zwischen den Landkreisen; BG: Breusch-Godfrey/Wooldridge-Test 1 = Autokorrelation; BP: Breusch-Pagan Test, 1 = Heteroskedastizität
(Sub)Nation | FF | HT | LM | BG | BP |
Winterweizen | |||||
Schleswig-Holstein | 0 | 1 | 1 | 1 | 1 |
Niedersachsen | 0 | 1 | 1 | 1 | 1 |
Nordrhein-Westfalen | 1 | 1 | 1 | 1 | 1 |
Hessen | 0 | 1 | 1 | 1 | 1 |
Rheinland-Pfalz | 0 | 0 | 1 | 1 | 1 |
Baden-Württemberg | 0 | 1 | 1 | 1 | 0 |
Bayern | 1 | 1 | 1 | 1 | 0 |
Saarland | 0 | – | 0 | 1 | 0 |
Brandenburg | 1 | 0 | 1 | 1 | 0 |
Mecklenburg-Vorpommern | 1 | 1 | 1 | 1 | 1 |
Sachsen | 0 | 1 | 1 | 1 | 0 |
Sachsen-Anhalt | 0 | 0 | 1 | 1 | 1 |
Thüringen | 1 | 1 | 1 | 1 | 1 |
Schlei/Trave | 0 | – | 1 | 1 | 0 |
Elbe | 1 | 0 | 1 | 1 | 1 |
Weser | 0 | 0 | 1 | 1 | 1 |
Ems | 0 | 1 | 1 | 1 | 0 |
Rhein | 0 | 1 | 1 | 1 | 1 |
Maas | 1 | – | 1 | 0 | 0 |
Donau | 0 | – | 1 | 1 | 0 |
Warnow/Peene | 1 | 1 | 1 | 1 | 1 |
Oder | 0 | – | 1 | 0 | 0 |
Deutschland | 1 | 1 | 1 | 1 | 1 |
Silomais | |||||
Schleswig-Holstein | 0 | 0 | 1 | 1 | 0 |
Niedersachsen | 0 | 0 | 1 | 1 | 0 |
Nordrhein-Westfalen | 0 | 0 | 1 | 1 | 0 |
Hessen | 0 | 0 | 1 | 1 | 0 |
Rheinland-Pfalz | 1 | 0 | 1 | 1 | 1 |
Baden-Württemberg | 1 | 1 | 1 | 1 | 0 |
Bayern | 1 | 1 | 1 | 1 | 1 |
Saarland | 1 | – | 0 | 0 | 1 |
Brandenburg | 1 | 0 | 1 | 1 | 0 |
Mecklenburg-Vorpommern | 1 | 1 | 1 | 1 | 0 |
Sachsen | 1 | 0 | 1 | 1 | 0 |
Sachsen-Anhalt | 1 | 0 | 1 | 1 | 0 |
Thüringen | 1 | 1 | 1 | 1 | 0 |
Schlei/Trave | 0 | – | 1 | 1 | 0 |
Elbe | 1 | 0 | 1 | 1 | 1 |
Weser | 0 | 0 | 1 | 1 | 1 |
Ems | 0 | 0 | 1 | 1 | 0 |
Rhein | 0 | 1 | 1 | 1 | 0 |
Maas | 0 | – | 1 | 0 | 0 |
Donau | 1 | 1 | 1 | 1 | 0 |
Warnow/Peene | 1 | 1 | 1 | 1 | 0 |
Oder | 0 | – | 1 | 0 | 0 |
Deutschland | 1 | 1 | 1 | 1 | 1 |
Asseng, S., F. Ewert, C. Rosenzweig, J.W. Jones, J.L. Hatfield, A.C. Ruane, K.J. Boote, P.J. Thorburn, R.P. Rotter, D. Cammarano, N. Brisson, B. Basso, P. Martre, P.K. Aggarwal, C. Angulo, P. Bertuzzi, C. Biernath, A.J. Challinor, J. Doltra, S. Gayler, R. Goldberg, R. Grant, L. Heng, J. Hooker, L.A. Hunt, J. Ingwersen, R.C. Izaurralde, K.C. Kersebaum, C. Muller, S. Naresh Kumar, C. Nendel, G. O'Leary, J.E. Olesen, T.M. Osborne, T. Palosuo, E. Priesack, D. Ripoche, M.A. Semenov, I. Shcherbak, P. Steduto, C. Stockle, P. Stratonovitch, T. Streck, I. Supit, F. Tao, M. Travasso, K. Waha, D. Wallach, J.W. White, J.R. Williams, J. Wolf, 2013: Uncertainty in simulating wheat yields under climate change. Nature Climate Change 3, 827-832.
Bakker, M.M., G. Govers, F. Ewert, M. Rounsevell, R. Jones, 2005: Variability in regional wheat yields as a function of climate, soil and economic variables: Assessing the risk of confounding. Agriculture, Ecosystems & Environment 110 (3-4), 195-209.
Beck, N., J.N. Katz, 2007: Random Coefficient Models for Time-Series-Cross-Section Data: Monte Carlo Experiments. Political Analysis 15, 182-195.
Bormann, H.B.D., O. Richter, 1996: Effects of Data Availability on Estimation of Evapotranspiration. Physics and Chemistry of the Earth 21 (3), 171-175.
Brisson, N., P. Gate, D. Gouache, G. Charmet, F.-X. Oury, F. Huard, 2010: Why are wheat yields stagnating in Europe? A comprehensive data analysis for France. Field Crops Research 119, 201-212.
Bristow, K.L., G.S. Campbell, 1984: On the relationship between incoming solar radiation and daily maximum and minimum temperature. Agricultural and Forest Meteorology 31, 159-166.
Butler, E.E., P. Huybers, 2013: Adaptation of US maize to temperature variations. Nature Climate Change 3, 68-72.
Castellvi, F., P.J. Perez, J.M. Villar, J.I. Rosell, 1996: Analysis of methods for estimating vapor pressure deficits and relative humidity. Agricultural and Forest Meteorology 82, 29-45.
Challinor, A.J., J. Watson, D.B. Lobell, S.M. Howden, D.R. Smith, N. Chhetri, 2014: A meta-analysis of crop yield under climate change and adaptation. Nature Climate Change 4, 287-291.
Chmielewski, F.-M., A. Müller, E. Bruns, 2004: Climate changes and trends in phenology of fruit trees and field crops in Germany, 1961–2000. Agricultural and Forest Meteorology 121, 69-78.
Chmielewski, F., W. Köhn, 2000: Impact of weather on yield components of winter rye over 30 years. Agricultural and Forest Meteorology 102, 253-261.
Croissant, Y., G. Millo, 2008: Panel Data Econometrics in R: The plm Package. Journal of Statistical Software 27 (2), 1-43.
Dielman, T.E., 1983: Pooled Cross-Sectional and Time Series Data: A Survey of Current Statistical Methodology. The American Statistician 37 (2), 111-122.
Dixon, B.L., S.E. Hollinger, P. Garcia, V. Tirupattur, 1994: Estimating Corn Yield Response Models to Predict Impacts of Climate Change. Journal of Agricultural and Resource Economics 19 (1), 58-68.
Doll, J.P., 1967: An Analytical Technique for Estimating Weather Indexes from Meteorological Measurements. Journal of Farm Economics 49 (1), 79-88.
Donatelli, M., G. Bellocchi, L. Carlini, 2006: Sharing knowledge via software components: Models on reference evapotranspiration. European Journal of Agronomy 24 (2), 186-192.
DVWK, 1996: Ermittlung der Verdunstung von Land- und Wasserflächen. DVWK-Merkblätter zur Wasserwirtschaft. Wirtschafts- und Verlagsgesellschaft Gas und Wasser mbH, Bonn, 240 S.
DWD, 2014: Aktueller Stand der Phänologie in Deutschland, 1992–2013. Deutscher Wetterdienst, Retrieved from: http://www.dwd.de/phaenologie (12.04.2015).
Garcia, P., S.E. Offutt, M. Pinar, S.A. Changing, 1987: Corn Yield Behavior – Effects of Technological Advance and Weather-Conditions. Journal of Climate and Applied Meteorology 26, 1092-1102.
Iizumi, T., H. Sakuma, M. Yokozawa, J.-J. Luo, A.J. Challinor, M.E. Brown, G. Sakurai, T. Yamagata, 2013: Prediction of seasonal climate-induced variations in global food production. Nature Climate Change 3, 904-908.
Kaufmann, R.K., S.E. Snell, 1997: A Biophysical Model of Corn Yield: Integrating Climatic and Social Determinants. American Journal of Agricultural Economics 79 (1), 178-190.
Kersebaum, K.C., C. Nendel, 2014: Site-specific impacts of climate change on wheat production across regions of Germany using different CO2 response functions. European Journal of Agronomy 52, 22-32.
Krause, J., 2008: A Bayesian approach to German agricultural yield expectations. Agricultural Finance Review 68, 9-23.
Krause, P., D.P. Boyle, F. Bäse, 2005: Comparison of different efficiency criteria for hydrological model assessment. Advances in Geosciences 5, 89-97.
Lee, B.-H., P. Kenkel, B.W. Brorsen, 2013: Pre-harvest forecasting of county wheat yield and wheat quality using weather information. Agricultural and Forest Meteorology 168, 26-35.
Lobell, D.B., 2010: Crop Responses to Climate: Time-Series Models. In: D.B. Lobell, M. Burke (Eds.): Climate Change and Food Security. Advances in Global Change Research, Vol. 37, Springer Netherlands, p. 85-98.
Lobell, D.B., 2013: Errors in climate datasets and their effects on statistical crop models. Agricultural and Forest Meteorology 170, 58-66.
Lobell, D.B., G.P. Asner, 2003: Climate and Management Contributions to Recent Trends in U.S. Agricultural Yields. Science 299 (5609), 1032.
Lobell, D.B., M.B. Burke, 2010: On the use of statistical models to predict crop yield responses to climate change. Agricultural and Forest Meteorology 150 (11), 1443-1452.
Lobell, D.B., G.L. Hammer, G. McLean, C. Messina, M.J. Roberts, W. Schlenker, 2013: The critical role of extreme heat for maize production in the United States. Nature Climate Change 3 (5), 497-501.
Lobell, D.B., W. Schlenker, J. Costa-Roberts, 2011: Climate trends and global crop production since 1980. Science 333 (6042), 616-620.
Monteith, J.L., 1977: Climate and the efficiency of crop production in Britain. Philosophical Transactions of the Royal Society of London 281, 277-294.
Moore, F.C., D.B. Lobell, 2014: Adaptation potential of European agriculture in response to climate change. Nature Climate Change, 4, 610-614.
Nendel, C., R. Wieland, W. Mirschel, X. Specka, C. Guddat, K.C. Kersebaum, 2013: Simulating regional winter wheat yields using input data of different spatial resolution. Field Crops Research 145, 67-77.
Oury, B., 1965: Allowing for Weather in Crop Production Model Building. Journal of Farm Economics 47 (2), 270-283.
Palosuo, T., K.C. Kersebaum, C. Angulo, P. Hlavinka, M. Moriondo, J.E. Olesen, R.H. Patil, F. Ruget, C. Rumbaur, J. Takáč, M. Trnka, M. Bindi, B. Çaldağ, F. Ewert, R. Ferrise, W. Mirschel, L. Şaylan, B. Šiška, R. Rötter, 2011: Simulation of winter wheat yield and its variability in different climates of Europe: A comparison of eight crop growth models. European Journal of Agronomy 35 (3), 103-114.
Reidsma, P., F. Ewert, A.O. Lansink, 2007: Analysis of farm performance in Europe under different climatic and management conditions to improve understanding of adaptive capacity. Climatic Change 84 (3-4), 403-422.
Roberts, M.J., W. Schlenker, J. Eyer, 2012: Agronomic weather measures in econometric models of crop yield with implications for climate change. American Journal of Agricultural Economics 95 (2), 236-243.
Schlenker, W., M.J. Roberts, 2009: Nonlinear temperature effects indicate severe damages to U.S. crop yields under climate change. Proceedings of the National Academy of Sciences of the United States of America 106 (37), 15594-15598.
Schrödter, H., 1985: Verdunstung: Anwendungsorientierte Meßverfahren und Bestimmungsmethoden. Berlin, Heidelberg,Springer, 204 S.
Shaw, L.H., 1964: The Effect of Weather on Agricultural Output: A Look at Methodology. Journal of Farm Economics 46 (1), 218-230.
Sonntag, D., 1990: Important new Values of the Physical Constants of 1986, Vapour Pressure Formulations based on ITS-90, and Psychrometer Formulae. Meteorologische Zeitschrift 4 (5), 340-344.
Statistisches Bundesamt, 2013: Ackerland nach Hauptfruchtgruppen und Fruchtarten, Land- & Forstwirtschaft, Fischerei – Feldfrüchte und Grünland.
Tannura, M.A., S.H. Irwin, D.L. Good, 2008: Weather, Technology, and Corn and Soybean Yields in the U.S. Corn Belt. Marketing and Outlook Research Report, Department of Agricultural and Consumer Economics, University of Illinois at Urbana-Champaign, 1-127.
Woodard, J.D., P. Garcia, 2008: Weather Derivatives, Spatial Aggregation, and Systemic Risk: Implications for Reinsurance Hedging. Journal of Agricultural and Resource Economics 33 (1), 34-51.
Wooldridge, J.M., 2013: Introductory Econometrics. A Modern Approach. South Western Cengage Learning, 868 S.
You, L., M.W. Rosegrant, S. Wood, D. Sun, 2009: Impact of growing season temperature on wheat productivity in China. Agricultural and Forest Meteorology 149 (6-7), 1009-1014.
Literatur zum Appendix
Bates, D., 2010: lme4: Mixed-effects modeling with R. Springer.
Croissant, Y., G. Millo, 2008: Panel Data Econometrics in R: The plm Package. Journal of Statistical Software 27 (2), 1-43.
DWD, 2011: Tägliche Wetterdaten, 1951-2010. Deutscher Wetterdienst.
Grothendieck, G., 2012: sqldf: Perform SQL selects on R data frames. R-Package, 0.4-6.4.
Nuzzo, R., 2014: Scientific method: Statistical errors – P values, the 'gold standard' of statistical validity, are not as reliable as many scientists assume. Nature Climate Change 506, 150-152.
RCore Team, 2013: R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, 3.0.0. R Foundation for Statistical Computing, Vienna, Austria.
Roberts, M.J., W. Schlenker, J. Eyer, 2012: Agronomic weather measures in econometric models of crop yield with implications for climate change. American Journal of Agricultural Economics 95 (2), 236-243.
Statistische Ämter des Bundes und der Länder, 2013: Index der Einkaufspreise landwirtschaftlicher Betriebsmittel, Index der Erzeugerpreise landwirtschaftlicher Produkte.
Statistische Ämter des Bundes und der Länder, 2013a: Datensatz Anbaufläche (Feldfrüchte und Grünland): Deutschland, Jahre, Fruchtarten 1991-2007.
Statistische Ämter des Bundes und der Länder, 2013b: Hektarerträge ausgewählter landwirtschaftlicher Feldfrüchte – Jahressumme – regionale Tiefe: Kreise und krfr. Städte.
Statistische Ämter des Bundes und der Länder, 2013c: Index der Erzeugerpreise landwirtschaftlicher Produkte.
Statistisches Bundesamt, 2013: Ackerland nach Hauptfruchtgruppen und Fruchtarten, Land- & Forstwirtschaft, Fischerei – Feldfrüchte und Grünland.
Studenmund, A.H., 2000: Using Econometrics: A Practical Guide, 4. Addison Wesley.
Wooldridge, J.M., 2013: Introductory Econometrics. A Modern Approach. South Western Cengage Learning, 868 S.
Zeileis, A., T. Hothorn, 2002: Diagnostic Checking in Regression Relationships.
Zeilleis, A., 2004: Econometric Computing with HC and HAC Covariance Matrix Estimators. Journal of Statistical Software 11 (10), 1-17.
Suchen
