

Die Gleitmethode nach Mitscherlich und was sie mit Geostatistik zu tun hat
Mitscherlich's slide method and what it has to do with geostatistics
Journal für Kulturpflanzen, 72 (10-11). S. 527–540, 2020, ISSN 1867-0911, DOI: 10.5073/JfK.2020.10-11.03, Verlag Eugen Ulmer KG, Stuttgart
 | Dies ist ein Open-Access-Artikel, der unter den Bedingungen der Creative Commons Namensnennung 4.0 International Lizenz (CC BY 4.0) zur Verfügung gestellt wird (https://creativecommons.org/licenses/by/4.0/deed.de). This is an Open Access article distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/deed.en). |
Die Mitscherlich-Anlage ist eine Versuchsanlage, bei der die Versuchsglieder in systematischer Reihenfolge in einer Reihe von Parzellen angeordnet sind. Diese Anordnung erlaubt es, mittels gleitender vollständiger Blöcke gleitende Mittelwerte über die gesamte Versuchsfläche zu berechnen. Diese Mittelwerte erfassen den räumlichen Trend und können zu einer Korrektur der Beobachtungswerte herangezogen werden. Dem Verfahren, das als Gleitmethode bekannt ist, wurde bei seiner Entwicklung allerdings kein explizites statistisches Modell zugrunde gelegt, so dass die Frage der zu bevorzugenden Auswertung solcher systematischen Versuchsanlagen offen ist. Des Weiteren stellen sich Fragen nach der relativen Vorzüglichkeit solcher Versuchsanlagen gegenüber randomisierten Versuchsanlagen und nach der besten Analysemethode. Diese Fragen sind insofern von aktueller Bedeutung, als es noch heute genutzte Langzeitversuche gibt, welche nach einem systematischen Design angelegt wurden. In diesem Beitrag gehen wir diesen Fragen nach, indem wir dem für die Gleitmethode vorgeschlagenen Auswertungsalgorithmus ein lineares gemischtes Modell zugrunde legen, welches eine lineare geostatistische Kovarianzstruktur impliziert. Wir betrachten dabei auch eine zweidimensionale Erweiterung des Mitscherlich-Verfahrens, welches von von Boguslawski unter der Bezeichnung „Ertragsflächenmethode“ vorgeschlagen wurde. Unsere Ergebnisse zeigen, dass ein systematisches Design unter dem hier vorgeschlagenen Modell tatsächlich optimal ist. Hieraus sollte allerdings nicht geschlossen werden, dass ein systematisches Design randomisierten Versuchsplänen vorzuziehen ist, denn es ist nicht zu erwarten, dass dieses spezielle Modell grundsätzlich besser an gegebene Daten passt als andere Vertreter aus der großen Klasse der geostatistischen Modelle. Die Vorteile einer Randomisation von Versuchen werden in der Schlussfolgerung betont.
Stichwörter: Mitscherlich-Anlage, Nächstnachbaranalyse, Geostatistik, Blockanlage, Zeilen-Spalten-Plan
The Mitscherlich design entails a systematic arrangement of the treatments in a single row of plots. This arrangement allows forming “sliding” complete blocks across the whole design, for which moving averages can be computed. These means capture spatial trend and may be employed for correcting the observed data. The method, which is known as “slide method”, does not have an underlying statistical model, meaning that the choice of best method for analysis remains an open question for these systematic designs. Furthermore, there is the question of the relative merit of a systematic design compared to randomized designs and that concerning the best method of analysis. These questions are of current interest because several long-term experiments laid out according to a systematic design are still in use today. In this contribution, we pursue these questions based on a newly proposed linear mixed model that can be thought of as underlying the slide method and which implies a linear geostatistical covariance structure. We also consider a two-dimensional extension of the Mitscherlich method, which von Boguslawski proposed under the term “response surface method”. Our results show that a systematic arrangement is indeed optimal under the assumed model. This should not be taken to imply, however, that a systematic design is generally to be preferred to randomized designs, because it is not to be expected that the model proposed here provides the best fit among the large class of geostatistical models to any given dataset. The advantages of a randomized experimental design are emphasized in the conclusion.
Key words: Mitscherlich design, Nearest neighbour analysis, geostatistics, block design, row-column design
Eine der ältesten Anlagen für Feldversuche ist die Mitscherlich-Anlage (1925; siehe auch hier: Möller-Arnold & Feichtinger, 1929; Wermke, 1959; von Lochow & Schuster, 1961). Bei dieser Anlage werden die Versuchsglieder (Behandlungen) in systematischer Reihenfolge nebeneinander geprüft. In Abb. 1 findet sich ein Beispiel mit fünf Behandlungen (A-E) in fünf Wiederholungen.
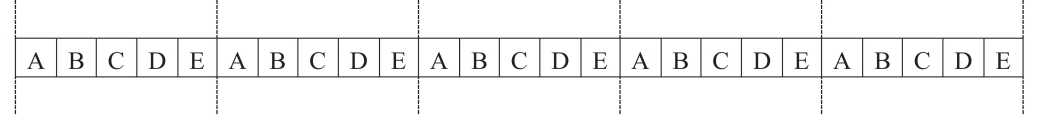
Abb. 1. Eine systematische Versuchsanlage (Mitscherlich-Anlage) mit fünf Behandlungen und fünf Wiederholungen für die Auswertung mit der Gleitmethode (von Lochow & Schuster, 1961, S. 5, Abb. 2).
Für die Ausgleichsrechnung mit der Gleitmethode nach Mitscherlich wird nun ein gleitendes Fenster der Größe eines vollständigen Blocks über die Anlage gelegt. So bilden die ersten fünf Parzellen in Abb. 1 einen vollständigen Block. Wird dieses Fenster um eine Parzelle nach rechts verschoben, ergibt sich wieder ein vollständiger Block. Der Mittelwert der jeweils fünf Prüfglieder des gleitenden Blocks liefert ein Maß für den räumlichen Trend der Ertragsfähigkeit von links nach rechts. Die beobachteten Ertragswerte können mit diesem Mittelwert korrigiert werden, typischerweise durch Differenzbildung (von Lochow & Schuster, 1961, S. 96ff.) oder Division (von Boguslawski, 1942). Solche korrigierten Werte werden für alle möglichen Platzierungen des gleitenden Blocks berechnet und dann je Behandlung gemittelt, um bereinigte Behandlungseffekte zu berechnen. Wird zu diesen Schätzwerten ein Gesamtmittelwert hinzuaddiert, ergeben sich korrigierte Behandlungsmittelwerte. Aus den einzelnen korrigierten Werten werden darüber hinaus Standardabweichungen und Standardfehler sowie Grenzdifferenzen für die Mittelwerte berechnet (von Lochow & Schuster, 1961, S.99).
Die Gleitmethode von Mitscherlich stellt ein Verfahren für Anlagen dar, bei denen die Parzellen wie in Abb. 1 in einer einzigen Reihe angeordnet sind. Es wurde von von Boguslawski (1942) für zweidimensionale Anlagen unter der Bezeichnung „Ertragsflächenmethode“ erweitert. Hierbei liegt der Fokus auf zwei Behandlungsfaktoren, von denen der eine systematisch in den Zeilen und der andere in den Spalten variiert wird. Das gleitende Fenster umfasst jeweils alle Behandlungen einmal, wobei die Zahl der Zeilen des Fensters der Zahl der Stufen des einen Faktors entspricht und die Zahl der Spalten der Zahl der Stufen des anderen Faktors. Die vorgeschlagene Analyse lehnt sich an die Gleitmethode von Mitscherlich an, wobei von Boguslawski für die Trendkorrektur Quotienten aus Parzellenwert und Mittelwert des gleitenden Blocks verwendet.
Die Gleitmethode von Mitscherlich wie auch die Ertragsflächenmethode von von Boguslawski bringen es mit sich, dass die Behandlungen systematisch angeordnet werden müssen und keinerlei Randomisation erfolgt, damit die gleitenden Blöcke jeweils vollständig sind. Damit stehen diese Methoden im Gegensatz zu der von R. A. Fisher (1925) eingeführten Methode zur Anlage von Feldversuchen, welche eine zufällige Zuordnung der Behandlungen zu den Parzellen erfordert. Da Fishers Prinzipien der Versuchsplanung sich inzwischen nicht nur in der Landwirtschaft als Standard etabliert haben (John & Williams, 1995; Thomas, 2006; Bailey, 2008), mag die Befassung mit den systematischen Versuchsanlagen nach Mitscherlich und von Boguslawski aus heutiger Sicht als von eher historischem Interesse erscheinen (Thomas, 2006). Es gibt allerdings noch aktuell laufende Dauerversuche, die nach diesen systematischen Plänen angelegt wurden und auch noch heute ausgewertet werden (Macholdt et al., 2019, 2020). Daher stellt sich die Frage nach der angemessenen Auswertung solcher Versuche weiterhin.
Ziel der vorliegenden Arbeit ist es, ein neues Licht auf die von Mitscherlich vorgeschlagene Auswertungsmethode zu werfen und eine Brücke zu moderneren geostatistischen Verfahren der Modellierung von Daten aus Feldversuchen zu schlagen. Nach einem einführenden Beispiel mit einem eindimensionalen Versuchsplan wird ein zweites Beispiel betrachtet, bei dem der Versuch in Zeilen und Spalten angelegt ist.
Mitscherlich (1925) hat kein lineares Modell für seine Methode formuliert. Es ist aber von Interesse die Frage zu klären, ob ein solches Modell formuliert werden kann. Denn wenn dies der Fall ist, weist dies einen Weg, wie nach der Gleitmethode und deren Erweiterung durch von Boguslawski (1942) angelegte Versuche mit heutigen Methoden ausgewertet werden können. Daher soll im Folgenden zunächst die Gleitmethode beschrieben und dann ein lineares Modell hergeleitet werden.
Die Grundidee der Gleitmethode von Mitscherlich ist, dass gleitende Blöcke es erlauben, die beobachteten Parzellendaten um Bodentrends zu bereinigen. Falls die Korrektur mit Differenzen erfolgt (von Lochow & Schuster, 1961, S. 96–97), so kann diese für einen gleitenden Block geschrieben werden als
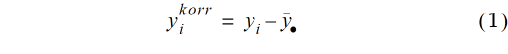
wobei yi der Parzellenwert für die i-te Behandlung ist (i = 1, 2,..., v) und
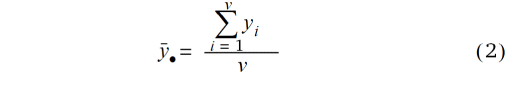
der arithmetische Mittelwert über alle v Beobachtungen des Blocks, wobei v gleich der Zahl der Behandlungen ist. Bei dieser Formulierung, welche lediglich einen einzigen gleitenden Block betrachtet, ist eine Indizierung für die Blöcke der Einfachheit halber weggelassen worden. Es wird außerdem vorausgesetzt, dass der gleitende Block jeweils ein vollständiger ist, dass also jede Behandlung genau einmal vorkommt.
Die Formulierung der Mitscherlich-Methode basiert ausschließlich auf Beobachtungswerten und deren direkter Verrechnung. Es gibt keinerlei statistisches Modell, welches von Mitscherlich explizit formuliert worden wäre, um sein Verfahren zu begründen oder herzuleiten. Allerdings impliziert die Betrachtung von vollständigen Blöcken zur Korrektur nach Gleichung (1), dass Blockmittelwerte es erlauben, einen räumlichen Trend zu erfassen. Der Blockmittelwert, um den die Parzellenwerte dabei korrigiert werden, kann als Trendwert aufgefasst werden. Um diesen Gedanken zu konkretisieren, ist es hilfreich, ein lineares Modell für die Parzellenwerte zu formulieren. Hierzu gehen wir zunächst von der Situation aus, dass auf allen Parzellen dieselbe Behandlung geprüft wird. Dies führt zu einem sog. Nullmodell (Nelder, 1965), also einem Modell, welches bei Abwesenheit von Behandlungseffekten gilt. Für einen betrachteten Block können wir das Mittel über die Parzellenwerte als Trendwert für den gesamten Block betrachten. Für diesen Trendwert kann das Modell  + b verwendet werden, wobei
+ b verwendet werden, wobei 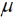 ein Gesamtmittel aller Parzellenwerte über den ganzen Versuch ist und b die Abweichung des Trendwertes für den betrachteten Block vom Gesamtmittel, also der Blockeffekt. Da es bei der Gleitmethode nicht nur einen gleitenden Block gibt, ist es sinnvoll, einen Index für den Block einzuführen. Dies führt dann zu dem Modell
ein Gesamtmittel aller Parzellenwerte über den ganzen Versuch ist und b die Abweichung des Trendwertes für den betrachteten Block vom Gesamtmittel, also der Blockeffekt. Da es bei der Gleitmethode nicht nur einen gleitenden Block gibt, ist es sinnvoll, einen Index für den Block einzuführen. Dies führt dann zu dem Modell 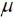 + bj für den im j-ten gleitenden Block für jede Parzelle erwarteten Beobachtungswert, wobei der Index von j = 1 bis zur Zahl der Blöcke läuft. Allerdings variieren die Beobachtungswerte innerhalb eines Blocks von Parzelle zu Parzelle. Um diese Schwankung abzubilden, führen wir einen Parzelleneffekt e ein, der auch als Parzellenfehler oder Residualeffekt bezeichnet wird. Das Nullmodell für den Beobachtungswert in der i-ten Behandlung im j-ten Block lautet dann
+ bj für den im j-ten gleitenden Block für jede Parzelle erwarteten Beobachtungswert, wobei der Index von j = 1 bis zur Zahl der Blöcke läuft. Allerdings variieren die Beobachtungswerte innerhalb eines Blocks von Parzelle zu Parzelle. Um diese Schwankung abzubilden, führen wir einen Parzelleneffekt e ein, der auch als Parzellenfehler oder Residualeffekt bezeichnet wird. Das Nullmodell für den Beobachtungswert in der i-ten Behandlung im j-ten Block lautet dann
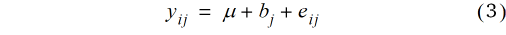
Bis hierher wurde angenommen, dass es keine Behandlungseffekte gibt. Wenn 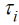 den Effekt der i-ten Behandlung bezeichnet, dann lautet das um diesen Effekt erweiterte Modell
den Effekt der i-ten Behandlung bezeichnet, dann lautet das um diesen Effekt erweiterte Modell
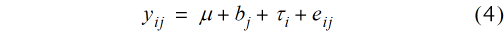
Nachdem nun ein lineares Modell für die Beobachtungswerte formuliert ist, können wir die Korrektur in Gl. (1) untersuchen, indem wir dieses Modell anstelle der Beobachtungswerte dort einsetzen, wobei der Index für den Blockeffekt hinzugefügt wird:
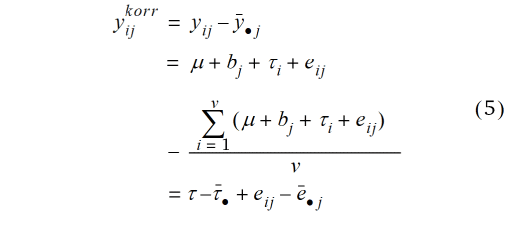
Offensichtlich bereinigt die Korrektur die Beobachtungswerte um die Trendwerte 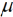 + bj. Dies ist die Kernidee des Verfahrens von Mitscherlich, auch wenn er für dessen Begründung kein lineares Modell verwendet hat.
+ bj. Dies ist die Kernidee des Verfahrens von Mitscherlich, auch wenn er für dessen Begründung kein lineares Modell verwendet hat.
Das Modell in Gleichung (4) ist unschwer zu erkennen als dasselbe Modell, welches auch für eine randomisierte vollständige Blockanlage verwendet wird (Fisher, 1925; John & Williams, 1995). Allerdings besteht ein wesentlicher Unterschied darin, dass eine Blockanlage disjunkte, also räumlich eindeutig getrennte Blöcke hat, während die Gleitmethode überlappende Blöcke betrachtet. Dies bedeutet, dass bei der Gleitmethode jede Parzelle nicht nur einem Block zuzuordnen ist, sondern v verschiedenen Blöcken. Diese Tatsache ist in Gleichung (4) so nicht abgebildet, weil wir bisher nur einen einzigen gleitenden Block betrachtet haben, weswegen dieses vereinfachte Modell verwendet werden konnte. Hierbei sind die Effekte der weiteren Blöcke, denen eine Parzelle im Gleitverfahren zugeordnet wird, durch den Residualeffekt eij subsumiert. Aber wegen der überlappenden Blöcke ist das Modell für die gesamte Anlage in dieser Form noch nicht vollständig und muss im Folgenden noch erweitert werden. Hierzu muss die mathematische Notation entsprechend modifiziert werden. Bisher wurde der Beobachtungswert nach dem Block j und der Behandlung i indiziert. Diese Indizierung wird jetzt ersetzt durch einen einzigen Index k für die Parzelle. Es ist dann yk der Beobachtungswert auf der k-ten Parzelle. Dabei läuft der Index k von 1 bis N, wobei N die Zahl der Parzellen des Versuchs bezeichnet. Ein lineares Modell, welches alle Effekte derjenigen Blöcke umfasst, denen die k-te Parzelle zugeordnet ist, kann wie folgt geschrieben werden:
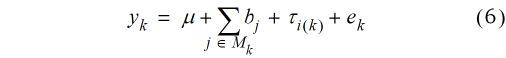
Hierin bezeichnet Mk die Menge aller Indices j für diejenigen gleitenden Blöcke, welche der k-ten Parzelle zugeordnet sind, i(k) ist der Index für die Behandlung, welche der k-ten Parzelle zugeordnet ist, 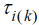 der dazugehörige Behandlungseffekt, und ek ist der Residualeffekt, also die Abweichung des k-ten Parzellenwertes yk vom erwarteten Wert
der dazugehörige Behandlungseffekt, und ek ist der Residualeffekt, also die Abweichung des k-ten Parzellenwertes yk vom erwarteten Wert
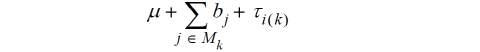
Da die Gleitmethode vollständige Blöcke verwendet, welche jeweils alle v Behandlungen umfassen, sind jedem gleitenden Block v Parzellen zugeordnet. Umgekehrt bedeutet dies auch, dass jeder Parzelle v verschiedene Blockeffekte zugeordnet sind, dass jede Menge Mk also v Blockindices umfasst. Dabei haben unmittelbar benachbarte Parzellen, die nur einen „Parzellenschritt“ von einander entfernt sind, jeweils v–1 Blockeffekte oder Trendwerte bj gemeinsam. Parzellen, die zwei Parzellenschritte voneinander entfernt sind, haben noch v–2 Blockeffekte gemeinsam, usw. Parzellen, die v Parzellenschritte oder mehr voneinander entfernt sind, haben keinen Blockeffekt mehr gemeinsam. Generell ist die Zahl der übereinstimmenden Blockeffekte für zwei Parzellen k und k' gegeben durch
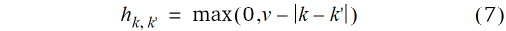
also gleich dem Maximum der Werte 0 und der Zahl der Behandlungen v abzüglich Parzellenschritte dk, k' = |k – k'|. Je mehr übereinstimmende Blockeffekte zwei Parzellen haben, um so ähnlicher sind sich die Beobachtungswerte gemäß dem Modell (6). Daher bildet dieses Modell die Erwartung ab, dass Parzellen um so ähnlichere Ertragsfähigkeit haben, je näher sie sich räumlich sind.
Der Vollständigkeit halber sei angemerkt, dass wir oben zwar die Annahme getroffen haben, dass jede Parzelle v Blocks zugeordnet ist, dass dies aber physisch offensichtlich nicht für die Randparzellen zutrifft. Jedoch ist es ohne weiteres möglich, von einer hypothetischen Erweiterung der Anlage nach links und rechts auszugehen dergestalt, dass auch die jeweils am Rande liegenden v–1 Parzellen jeweils v (zum Teil hypothetischen) Blöcken zugeordnet werden können. Damit lässt sich das aus unserem Ansatz hergeleitete Modell tatsächlich auf alle Parzellen anwenden.
Damit sind wir bei einer Betrachtungsweise angelangt, wie sie in der Geostatistik geläufig ist. Um diese Betrachtungsweise konsequent zu Ende zu führen, ist es erforderlich, Verteilungsannahmen zu machen. Hier sind natürlich verschiedene Optionen denkbar, aber die naheliegendste Annahme ist die folgende: (i) Für die Parzellenfehler ek kann angenommen werden, dass sie zwischen den Parzellen unabhängig sind und Varianz  haben. (ii) Für die zufälligen Blockeffekte bj wird angenommen, dass sie zwischen den Blöcken unabhängig sind und die Varianz
haben. (ii) Für die zufälligen Blockeffekte bj wird angenommen, dass sie zwischen den Blöcken unabhängig sind und die Varianz 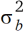 haben. Die Unabhängigkeitsannahme mag für die Blockeffekte auf den ersten Blick unrealistisch erscheinen wegen des zu erwartenden räumlichen Trends. Hier ist aber zu berücksichtigen, dass es überlappende Blöcke gibt, und dies induziert bei diesem Modell eine räumliche Abhängigkeit auch zu Parzellen in benachbarten Blöcken, wie im Folgenden erläutert wird. Da jeder Parzelle v Blockeffekte zugeordnet sind, ist die Varianz eines Beobachtungswertes mit diesen Annahmen
haben. Die Unabhängigkeitsannahme mag für die Blockeffekte auf den ersten Blick unrealistisch erscheinen wegen des zu erwartenden räumlichen Trends. Hier ist aber zu berücksichtigen, dass es überlappende Blöcke gibt, und dies induziert bei diesem Modell eine räumliche Abhängigkeit auch zu Parzellen in benachbarten Blöcken, wie im Folgenden erläutert wird. Da jeder Parzelle v Blockeffekte zugeordnet sind, ist die Varianz eines Beobachtungswertes mit diesen Annahmen
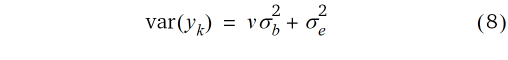
Parzellen mit übereinstimmenden Blockeffekten haben außerdem eine Kovarianz. So haben zwei benachbarte Parzellen wie oben bemerkt v–1 Blockeffekte gemeinsam und daher eine Kovarianz von 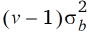 . Bei zwei Parzellenschritten beträgt die Kovarianz noch
. Bei zwei Parzellenschritten beträgt die Kovarianz noch 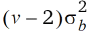 usw. Im allgemeinen ist die Kovarianz gleich
usw. Im allgemeinen ist die Kovarianz gleich
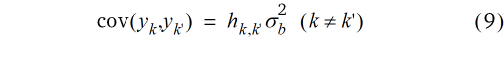
wobei hk, k' in Gleichung (7) angegeben ist. Je höher die Kovarianz, desto ähnlicher sind die beiden Parzellen k und k' in den Beobachtungswerten. Nach v Parzellenschritten von der k-ten zur k'-ten Parzelle ist die Kovarianz gleich Null. Bis zu diesem Abstand, der Reichweite (engl. range) des Modells, fällt die Kovarianz linear mit dem Abstand ab, um dann beim Wert Null stehen zu bleiben (Abb. 2).
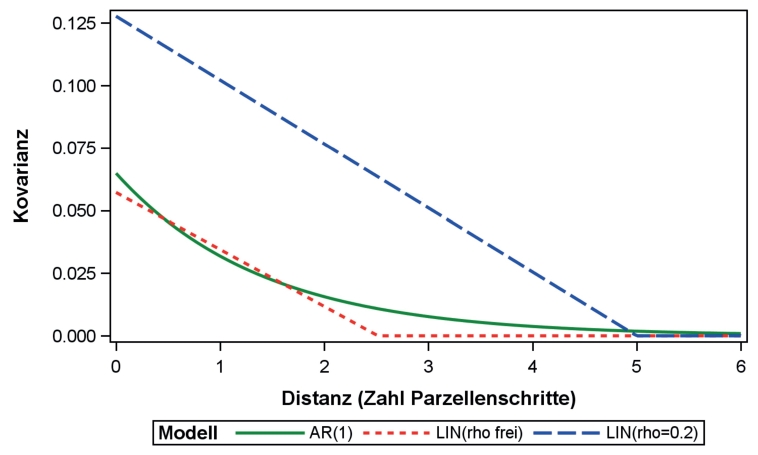
Abb. 2. Kovarianzfunktionen für drei geostatistische Modelle für das erste Beispiel (Parameterschätzwerte aus Tab. 2). AR(1) = autoregressives Modell erster Ordnung; LIN = lineares geostatistisches Modell (rho frei: ρ geschätzt mit der REML Methode; rho = 0.2: Fixierung ρ = 1/5).
Dieses Muster einer mit dem Abstand sinkenden Kovarianz ist charakteristisch für eine Vielzahl von Modellen der Geostatistik, welche sich lediglich in der genauen funktionalen Form dieses Abfallens der Kovarianz unterscheiden. Die Stärke des Abfallens hängt dabei von den Modellparametern ab. Je schneller der Abfall erfolgt, desto geringer ist die Reichweite der räumlichen Korrelation. Die meisten Modelle nehmen einen nichtlinearen Verlauf der Kovarianzfunktion an (Schabenberger & Gotway, 2005; für eine anwendungsorientierte Einführung siehe auch Slaets et al., 2020). Das hier beschriebene Modell ist dagegen ein Spezialfall des linearen Kovarianzmodells der Geostatistik (Williams, 1986). Die Reichweite dieses linearen geostatistischen Modells ist gegeben durch die Größe der gleitenden Blöcke und somit durch die Zahl der Behandlungen fixiert. Es besteht allerdings kein Grund zu der Annahme, dass dies der beste anzunehmende Wert für die Reichweite ist. Besser ist es, andere Werte für die Reichweite zuzulassen und den optimalen Wert aus den Daten zu schätzen. Dies kann mit Standardverfahren wie der Residual Maximum Likelihood (REML) Methode erfolgen (Schabenberger & Gotway, 2005). Es ist außerdem möglich Modelle anzupassen, welche anstatt eines linearen einen nichtlinearen Abfall der Kovarianz mit der räumlichen Distanz annehmen. Diese Betrachtungen stellen die Gleitmethode von Mitscherlich in einem gemeinsamen Zusammenhang mit geostatistischen Methoden, die heute routinemäßig für die Analyse von Feldversuchen eingesetzt werden (Gilmour et al., 1997; Piepho et al., 2008; Rodríguez-Álvarez et al., 2018). Wegen seiner Linearität besteht eine besonders enge Beziehung zu Verfahren der sog. Nächstnachbaranalyse, deren Entwicklung parallel mit der Erfindung der Varianzanalyse in den 30er Jahren des letzten Jahrhunderts vor allem im angelsächsischen Bereich ihren Anfang nahm und die auch heute noch eine große Bedeutung hat (Piepho et al., 2008).
Ein lineares Kovarianzmodell wird allerdings nicht zum selben Analyseergebnis führen wie die Gleitmethode von Mitscherlich, selbst wenn die Kovarianz-Struktur der Gleichungen (8) und (9) angenommen wird. Es ist nicht ohne weiteres klar, welches Analyseverfahren die besseren Ergebnisse liefert. Für den geostatistischen Ansatz spricht allerdings, dass ihm ein statistisches Modell zugrunde gelegt werden kann, während es für die Gleitmethode von Mitscherlich in der ursprünglich vorgeschlagenen Form kein Modell gibt. Auf Basis eines wohldefinierten statistischen Modells kann auch eine statistische Analyse mit etablierten Verfahren durchgeführt werden, während es für die Gleitmethode keine solche Basis gibt. Zwar wird bei von Lochow & Schuster (1961) vorgeschlagen, wie Standardfehler und Grenzdifferenzen für Behandlungsmittelwerte berechnet werden können, es besteht aber wegen des fehlenden Modells keine Basis für die Ableitung einer weitergehenden inferenz-statistischen Analyse, etwa mit einer Varianzanalyse oder multiplen Mittelwertvergleichen. Diese Lücke wird durch den hier gemachten Brückenschlag zur Geostatistik geschlossen.
Zur Illustration wird das bei von Lochow & Schuster (1961, S. 97) zur Erläuterung der Gleitmethode angegebene Beispiel verwendet. Es hat v = 5 Behandlungen und sechs Wiederholungen. Die Rohdaten sind in Tab. 1 wiedergegeben. Die Anpassung des linearen geostatistischen Modells erfolgt mit der SAS Prozedur MIXED über die Option type = sp(lin) mit der REML-Methode.
Tab. 1. Rohdaten für Beispiel aus von Lochow & Schuster (1961, S. 96–97) (erstes Beispiel). Winterraps; Teilstückerträge (in kg) bei 86 % Trockensubstanz; Teilstückgröße 20 qm.
Parzelle (k) | Behandlung | Ertrag |
1 | A | 5.26 |
2 | B | 5.18 |
3 | C | 4.78 |
4 | D | 5.85 |
5 | E | 5.50 |
6 | A | 5.76 |
7 | B | 5.76 |
8 | C | 5.18 |
9 | D | 5.94 |
10 | E | 5.05 |
11 | A | 5.51 |
12 | B | 5.38 |
13 | C | 4.50 |
14 | D | 5.91 |
15 | E | 5.38 |
16 | A | 5.70 |
17 | B | 5.50 |
18 | C | 4.71 |
19 | D | 5.52 |
20 | E | 4.74 |
21 | A | 5.66 |
22 | B | 5.72 |
23 | C | 5.17 |
24 | D | 5.91 |
25 | E | 5.48 |
26 | A | 5.16 |
27 | B | 5.14 |
28 | C | 4.70 |
29 | D | 5.82 |
30 | E | 5.03 |
Die Kovarianz nach dem linearen geostatistischen Modell ist in der MIXED Prozedur wie folgt parametrisiert:
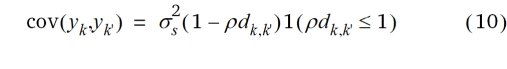
Hierbei ist 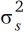 eine räumliche Varianzkomponente, dk,k' = |k – k'| ist die Distanz zwischen den Parzellen k und k', und
eine räumliche Varianzkomponente, dk,k' = |k – k'| ist die Distanz zwischen den Parzellen k und k', und 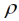 ist ein Parameter, der den Abfall der Kovarianz mit der Distanz bestimmt. Die Funktion 1(.) ist die Indikator-Funktion, welche den Wert 1 annimmt, falls der Ausdruck im Argument wahr ist und sonst den Wert 0. Dieser Faktor stellt hier sicher, dass die Kovarianz Null wird, wenn
ist ein Parameter, der den Abfall der Kovarianz mit der Distanz bestimmt. Die Funktion 1(.) ist die Indikator-Funktion, welche den Wert 1 annimmt, falls der Ausdruck im Argument wahr ist und sonst den Wert 0. Dieser Faktor stellt hier sicher, dass die Kovarianz Null wird, wenn 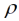 dk,k' > 1 wird. Ein Koeffizientenvergleich mit Gleichung (9) führt zu den Entsprechungen
dk,k' > 1 wird. Ein Koeffizientenvergleich mit Gleichung (9) führt zu den Entsprechungen 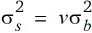 und
und 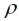 = v–1. Hierbei stellt die Spezifikation
= v–1. Hierbei stellt die Spezifikation 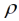 = v–1 sicher, dass für Parzellen mit dk,k' = |k – k'| = v, also für Parzellen, die v Parzellenschritte voneinander entfernt sind,
= v–1 sicher, dass für Parzellen mit dk,k' = |k – k'| = v, also für Parzellen, die v Parzellenschritte voneinander entfernt sind, 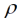 dk,k' = 1 ist und somit die Kovarianz gerade auf Null abgefallen ist. Alternativ kann der Reichweiten-Parameter
dk,k' = 1 ist und somit die Kovarianz gerade auf Null abgefallen ist. Alternativ kann der Reichweiten-Parameter 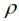 mit der REML-Methode auch aus den Daten geschätzt werden.
mit der REML-Methode auch aus den Daten geschätzt werden.
Die Varianzparameterschätzwerte nach dem linearen geostatistischen Modell sind in Tab. 2 angegeben. Zum Vergleich haben wir auch das AR(1)-Modell angepasst (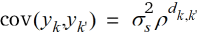 ; Piepho et al., 2015b), ein Modell mit unabhängigen Fehlern sowie ein Modell für eine Bockanlage mit zufälligen Effekten für sechs disjunkte Blöcke. Das AR(1)-Modell ist das am häufigsten verwendete nichtlineare geostatistische Modell für Feldversuche (Gilmour et al., 1997), weswegen es hier betrachtet wird. Bei diesem Modell sinkt die Kovarianz exponentiell mit dem räumlichen Abstand (Abb. 2). Gängige Maße für die Güte der Modellanpassung bei Verwendung der Likelihood-Methode sind die Devianz (minus der zweifache Wert der residualen logarithmierten Likelihood; je kleiner der Wert, umso besser die Anpassung) und das Akaikesche Informationskriterium (AIC = Devianz + 2p, wobei p = Zahl der Varianzparameter; je kleiner der Wert, umso besser das Modell; Wolfinger, 1996). Die Devianzen wie auch die AIC-Werte in Tab. 2 zeigen, dass die geostatistischen Modelle für diesen Datensatz vergleichsweise gut passen. Die Kovarianzfunktionen nach den geostatistischen Modellen aus Tab. 2 sind in Abb. 2 dargestellt. Es ist erkennbar, dass nach allen diesen Modellen die Kovarianz mit der Distanz sinkt. Dabei ist die Übereinstimmung des AR(1)-Modells mit dem linearen Modell relativ gut, wenn der Parameter des letzteren frei geschätzt wird (rote, gestrichelte Linie), während mit der Fixierung bei
; Piepho et al., 2015b), ein Modell mit unabhängigen Fehlern sowie ein Modell für eine Bockanlage mit zufälligen Effekten für sechs disjunkte Blöcke. Das AR(1)-Modell ist das am häufigsten verwendete nichtlineare geostatistische Modell für Feldversuche (Gilmour et al., 1997), weswegen es hier betrachtet wird. Bei diesem Modell sinkt die Kovarianz exponentiell mit dem räumlichen Abstand (Abb. 2). Gängige Maße für die Güte der Modellanpassung bei Verwendung der Likelihood-Methode sind die Devianz (minus der zweifache Wert der residualen logarithmierten Likelihood; je kleiner der Wert, umso besser die Anpassung) und das Akaikesche Informationskriterium (AIC = Devianz + 2p, wobei p = Zahl der Varianzparameter; je kleiner der Wert, umso besser das Modell; Wolfinger, 1996). Die Devianzen wie auch die AIC-Werte in Tab. 2 zeigen, dass die geostatistischen Modelle für diesen Datensatz vergleichsweise gut passen. Die Kovarianzfunktionen nach den geostatistischen Modellen aus Tab. 2 sind in Abb. 2 dargestellt. Es ist erkennbar, dass nach allen diesen Modellen die Kovarianz mit der Distanz sinkt. Dabei ist die Übereinstimmung des AR(1)-Modells mit dem linearen Modell relativ gut, wenn der Parameter des letzteren frei geschätzt wird (rote, gestrichelte Linie), während mit der Fixierung bei 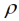 = 1/5 die Übereinstimmung weniger gut ausfällt. In Tab. 3 finden sich die Behandlungsmittelwerte nach verschiedenen Verfahren und Tab. 4 zeigt die paarweisen Differenzen der Behandlungsmittelwerte nach dem linearen geostatistischen Modell bei Schätzung des Reichweitenparameters
= 1/5 die Übereinstimmung weniger gut ausfällt. In Tab. 3 finden sich die Behandlungsmittelwerte nach verschiedenen Verfahren und Tab. 4 zeigt die paarweisen Differenzen der Behandlungsmittelwerte nach dem linearen geostatistischen Modell bei Schätzung des Reichweitenparameters 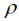 und bei dessen Fixierung beim Wert
und bei dessen Fixierung beim Wert 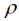 = 1/5. In Tab. 3 sind zum Vergleich außerdem die arithmetischen Mittelwerte sowie die in von Lochow & Schuster (1961) mit der Gleitmethode berechneten Mittelwerte aufgeführt. Für das lineare geostatistische Modell finden wir mit fixiertem Reichweiten-Parameter eine etwas höhere und damit schlechtere Devianz als bei freier Schätzung mit
= 1/5. In Tab. 3 sind zum Vergleich außerdem die arithmetischen Mittelwerte sowie die in von Lochow & Schuster (1961) mit der Gleitmethode berechneten Mittelwerte aufgeführt. Für das lineare geostatistische Modell finden wir mit fixiertem Reichweiten-Parameter eine etwas höhere und damit schlechtere Devianz als bei freier Schätzung mit 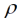 = 0.398 (Tab. 2). Die geschätzte Reichweite (1/
= 0.398 (Tab. 2). Die geschätzte Reichweite (1/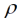 Parzellenschritte; bei dieser Distanz ist die Kovarianz auf Null gesunken) ist etwa halb so weit wie für das Modell mit fixiertem
Parzellenschritte; bei dieser Distanz ist die Kovarianz auf Null gesunken) ist etwa halb so weit wie für das Modell mit fixiertem 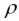 ; nach etwa nach 2.5 Parzellenschritten ist die Kovarianz bereits auf Null abgesunken (Abb. 1), was ein ähnlich schneller Abfall ist wie beim AR(1)-Modell, bei dem die Kovarianz sich allerdings nur asymptotisch der Null nähert. Wegen der geringen Reichweite bei Schätzung des Parameters
; nach etwa nach 2.5 Parzellenschritten ist die Kovarianz bereits auf Null abgesunken (Abb. 1), was ein ähnlich schneller Abfall ist wie beim AR(1)-Modell, bei dem die Kovarianz sich allerdings nur asymptotisch der Null nähert. Wegen der geringen Reichweite bei Schätzung des Parameters 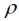 liegen die adjustieren Mittelwerte relativ nahe bei den arithmetischen Mittelwerten (Tab. 3). Die paarweisen Differenzen der Behandlungsmittelwerte haben bemerkenswerterweise für beide linearen geostatistischen Modelle relativ ähnliche Varianzen (Tab. 4). Die kompletten SAS Anweisungen sind im Elektronischen Anhang verfügbar, sowohl für das erste Beispiel als auch für das später folgende zweite Beispiel.
liegen die adjustieren Mittelwerte relativ nahe bei den arithmetischen Mittelwerten (Tab. 3). Die paarweisen Differenzen der Behandlungsmittelwerte haben bemerkenswerterweise für beide linearen geostatistischen Modelle relativ ähnliche Varianzen (Tab. 4). Die kompletten SAS Anweisungen sind im Elektronischen Anhang verfügbar, sowohl für das erste Beispiel als auch für das später folgende zweite Beispiel.
Tab. 2. Parameterschätzwerte (REML) für das lineare geostatistische Modell mit fixiertem (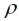 = v–1 = 0.2) und mit geschätztem Reichweitenparameter sowie weitere Modelle [AR(1)-Modell, Modell einer Blockanlage, Modell mit unabhängigen Fehlern] für das erste Beispiel.
= v–1 = 0.2) und mit geschätztem Reichweitenparameter sowie weitere Modelle [AR(1)-Modell, Modell einer Blockanlage, Modell mit unabhängigen Fehlern] für das erste Beispiel.
Parameter/ | LIN(ρ=1/5)a | LINa | AR(1) | Blockanlageb | Unabhängige Fehlerc |
| 0.1277 | 0.05719 | 0.06485 | – | – |
| – | – | – | 0.01840 | – |
| 0.2000 | 0.3975 | 0.4910 | – | – |
| 0 | 0.008777 | 0.000019 | 0.04627 | 0.06467 |
Devianz | 3.4 | 3.7 | 4.9 | 8.5 | 11.4 |
AIC | 5.4 | 9.7 | 10.9 | 12.5 | 13.4 |
a Kovarianz-Struktur in Gleichung (10). | |||||
Tab. 3. Behandlungsmittelwerte für das erste Beispiel bei Verwendung des linearen geostatistischen Modells mit fixiertem (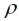 = v–1 = 0.2) und mit geschätztem Reichweitenparameter.
= v–1 = 0.2) und mit geschätztem Reichweitenparameter.
Behandlung | Arithmetisches | Gleitmethode |
| LIN(ρ=1/5)c |
| LINd | ||
Adjustierter Mittelwert | Adjustierter | Standardfehler | Adjustierter Mittelwert | Standardfehler | ||||
A | 5.5083 | 5.56 |
| 5.5329 | 0.1382 |
| 5.4930 | 0.1027 |
B | 5.4467 | 5.51 |
| 5.4607 | 0.1400 |
| 5.4401 | 0.1045 |
C | 4.8400 | 4.87 |
| 4.8095 | 0.1406 |
| 4.8400 | 0.1049 |
D | 5.8250 | 5.83 |
| 5.7862 | 0.1400 |
| 5.8207 | 0.1045 |
E | 5.1967 | 5.23 |
| 5.1462 | 0.1382 |
| 5.1780 | 0.1027 |
a Diese Mittelwerte entsprechen denen bei Auswertung nach einer Blockalage sowie nach | ||||||||
Tab. 4. Paarweise Vergleiche der fünf Behandlungen für das erste Beispiel für das lineare geostatistische Modell mit fixiertem und mit geschätztem Reichweitenparameter.
Vergleich | LIN(ρ=1/5)a |
| LINa |
| AR(1) | |||
| Adjustierte | Standardfehler |
| Adjustierte | Standardfehler |
| Adjustierte | Standardfehler |
A – B | 0.0722 | 0.02737 |
| 0.0529 | 0.1015 |
| 0.0566 | 0.1031 |
A – C | 0.7234 | 0.03424 |
| 0.6530 | 0.1328 |
| 0.6626 | 0.1221 |
A – D | –0.2533 | 0.03564 |
| –0.3277 | 0.1349 |
| –0.3190 | 0.1233 |
A – E | 0.3867 | 0.03228 |
| 0.3150 | 0.1070 |
| 0.3187 | 0.1077 |
B – C | 0.6511 | 0.02737 |
| 0.6001 | 0.1021 |
| 0.6060 | 0.1034 |
B – D | –0.3256 | 0.03424 |
| –0.3806 | 0.1339 |
| –0.3755 | 0.1226 |
B – E | 0.3145 | 0.03564 |
| 0.2621 | 0.1349 |
| 0.2621 | 0.1233 |
C – D | –0.9767 | 0.02737 |
| –0.9807 | 0.1021 |
| –0.9816 | 0.1034 |
C – E | –0.3366 | 0.03424 |
| –0.3380 | 0.1328 |
| –0.3439 | 0.1221 |
D – E | 0.6401 | 0.02737 |
| 0.6427 | 0.1015 |
| 0.6377 | 0.1031 |
Ø |
| 0.03158 |
|
| 0.1184 |
|
| 0.1134 |
a Lineares geostatistisches Modell mit Kovarianz | ||||||||
Die systematische Anordnung der Behandlungen ist bei der Mitscherlich-Methode eine Notwendigkeit, die sicherstellt, dass alle gleitenden Blöcke vollständig sind, also alle Behandlungen umfassen. Eine solche systematische Anordnung der Behandlungen war vor dem Computerzeitalter die einfachste Möglichkeit, eine Trendkorrektur durchzuführen, weil je gleitendem Block lediglich ein einfacher Mittelwert für die Korrektur zu berechnen ist. Aus heutiger Sicht besteht jedoch keine Notwendigkeit mehr für solch restriktive Versuchsanordnungen. Hinzu kommt natürlich, dass bei einer systematischen Anordnung keinerlei Randomisation möglich ist, was einem der Fisherschen Prinzipen der Versuchsplanung widerspricht (Fisher, 1925).
Die Nähe des Mitscherlichschen Ansatzes zu geostatistischen Modellen bietet allerdings die Möglichkeit, die genannten Restriktionen auf ihre Implikationen für die Effizienz des Designs hin zu untersuchen. Eine wichtige Forderung beim Design von Versuchen ist, dass alle paarweisen Behandlungsvergleiche möglichst mit derselben Genauigkeit durchgeführt werden können. Unter einem geostatistischen Modell ist die Varianz einer Differenz zweier Parzellenwerte um so kleiner je näher die Parzellen für die beiden Behandlungen beieinanderliegen. Bei einer systematischen Anordnung wie in Abb. 1 ist jede Behandlung immer von denselben anderen Behandlungen umgeben. Die Behandlung C in Abb. 1 findet sich zum Beispiel immer in der direkten Nachbarschaft der Behandlungen B und D. Dagegen ist die Behandlung C nie in direkter Nachbarschaft zu den Behandlungen A und E. Daher könnte erwartet werden, dass Vergleiche von C mit B und D genauer sind als die Vergleiche von C mit den Behandlungen A und E, was gegen die die systematische Anordnung sprechen könnte, abgesehen von der fehlenden Randomisierung. Zwar zeigte die Analyse für das erste Beispiel, dass die Standardfehler einer Differenz bei dem angenommenen linearen geostatistischen Modell relativ homogen sind, aber diese folgen trotzdem dem erwarteten Muster, da die Vergleiche A-B, B-C, C-D und D-E die kleineren Standardfehler haben (Tab. 4). Die Ergebnisse für Vergleiche der Behandlungsmittelwerte nach dem AR(1)-Modell sind relativ ähnlich denen nach dem linearen geostatistischen Modell mit geschätztem Wert für den Parameter 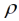 . Die Standardfehler einer Differenz für das Modell einer Blockanlage und das Modell mit unabhängigen Fehlern betragen 0.1242 und 0.1468. Diese Werte liegen höher als die durchschnittlichen Standardfehler einer Differenz nach den geostatistischen Modellen in Tab. 4.
. Die Standardfehler einer Differenz für das Modell einer Blockanlage und das Modell mit unabhängigen Fehlern betragen 0.1242 und 0.1468. Diese Werte liegen höher als die durchschnittlichen Standardfehler einer Differenz nach den geostatistischen Modellen in Tab. 4.
Interessant ist es in diesem Zusammenhang zu fragen, was unter dem oben abgeleiteten linearen geostatistischen Modell das optimale Design ist. Es ist mit heute gängigen numerischen Verfahren möglich, für jedes vorgegebene Modell bezüglich der Varianzen und Kovarianzen zwischen den Parzellen ein jeweils optimales Design zu suchen. Dazu wird jeweils ein Zielkriterium definiert, welches in der computer-gestützten Suche optimiert wird. Zwei gängige Kriterien sind die D-Effizienz und die A-Effizienz (John & Williams, 1995). Beide beruhen auf der sog. Informations-Matrix der Behandlungsmittelwerte. Die D-Effizienz entspricht der Determinante dieser Matrix, und das Ziel ist diese zu maximieren. Die A-Effizienz betrachtet die durchschnittliche paarweise Varianz einer Mittelwertdifferenz und das Ziel ist diese zu minimieren.
Wenn wir nun für das im vorangegangenen Abschnitt analysierte Beispiel die geschätzte Varianzstruktur für das lineare geostatistische Modell mit fixiertem Reichweiteparameter 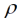 = 1/5 zugrunde legen und das optimale Design für fünf Behandlungen mit jeweils sechs Wiederholungen suchen, so finden wir für beide Kriterien die systematische Anordnung wie in Abb. 1 als das optimale Design! Dabei haben wir im Fall der D-Optimalität mit der SAS Prozedur OPTEX gerechnet (Piepho, 2015) und im Fall der A-Optimalität mit einem selbstgeschriebenen Programm in der Programmiersprache Julia (Vo-Thanh & Piepho, 2020). Dieses Resultat ist für uns, wie vermutlich auf für die Leser und Leserinnen auch, auf den ersten Blick sehr überraschend gewesen. Es bedeutet in gewisser Weise eine nachträgliche zusätzliche Rechtfertigung für den systematischen Ansatz der Mitscherlichschen Methode, denn legen wir das besagte lineare geostatistische Modell zugrunde, das wir hier hergeleitet haben, passen Auswertung und Design gewissermaßen optimal zusammen. Allerdings muss einschränkend angemerkt werden, dass das genannte Modell nicht notwendigerweise das für einen Datensatz am besten passende ist, und andere geostatistische Modelle führen zu anderen optimalen Designs (Cullis et al., 2006; Williams & Piepho, 2013). Und die weiterhin wichtigste Methode zur Design-Generierung, nämlich für die randomisierte vollständige Blockanlage mit disjunkten Blöcken, legt kein geostatistisches Modell zugrunde, sondern ein lineares Modell mit Blockeffekten (John & Williams, 1995). Es gibt auch keinen Grund davon auszugehen, dass unter den vielen möglichen geostatistischen Modellen (Schabenberger & Gotway, 2005) ausgerechnet das lineare Modell, und dann auch noch mit einem Reichweiteparameterwert von genau
= 1/5 zugrunde legen und das optimale Design für fünf Behandlungen mit jeweils sechs Wiederholungen suchen, so finden wir für beide Kriterien die systematische Anordnung wie in Abb. 1 als das optimale Design! Dabei haben wir im Fall der D-Optimalität mit der SAS Prozedur OPTEX gerechnet (Piepho, 2015) und im Fall der A-Optimalität mit einem selbstgeschriebenen Programm in der Programmiersprache Julia (Vo-Thanh & Piepho, 2020). Dieses Resultat ist für uns, wie vermutlich auf für die Leser und Leserinnen auch, auf den ersten Blick sehr überraschend gewesen. Es bedeutet in gewisser Weise eine nachträgliche zusätzliche Rechtfertigung für den systematischen Ansatz der Mitscherlichschen Methode, denn legen wir das besagte lineare geostatistische Modell zugrunde, das wir hier hergeleitet haben, passen Auswertung und Design gewissermaßen optimal zusammen. Allerdings muss einschränkend angemerkt werden, dass das genannte Modell nicht notwendigerweise das für einen Datensatz am besten passende ist, und andere geostatistische Modelle führen zu anderen optimalen Designs (Cullis et al., 2006; Williams & Piepho, 2013). Und die weiterhin wichtigste Methode zur Design-Generierung, nämlich für die randomisierte vollständige Blockanlage mit disjunkten Blöcken, legt kein geostatistisches Modell zugrunde, sondern ein lineares Modell mit Blockeffekten (John & Williams, 1995). Es gibt auch keinen Grund davon auszugehen, dass unter den vielen möglichen geostatistischen Modellen (Schabenberger & Gotway, 2005) ausgerechnet das lineare Modell, und dann auch noch mit einem Reichweiteparameterwert von genau 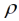 = 1/v am besten an die Daten passt. Daher möchten wir aus diesem interessanten und in der Tat überraschenden Ergebnis nicht den Schluss ziehen, dass ein systematisches Design vorzuziehen sei. Unsere Empfehlung ist, trotz dieses Befundes, so weit als möglich den Fisherschen Prinzipien zu folgen (Rundfeldt, 1953; John & Williams, 1995; Bailey, 2008). Im vorliegenden Fall würde dies weiterhin natürlich zur Empfehlung einer randomisierten vollständigen Blockanlage führen. Wir werden aber die Design-Frage im Folgenden wieder aufgreifen, wenn wir die Erweiterung der Mischerlichschen Gleitmethode auf den zweidimensionalen Fall betrachtet haben.
= 1/v am besten an die Daten passt. Daher möchten wir aus diesem interessanten und in der Tat überraschenden Ergebnis nicht den Schluss ziehen, dass ein systematisches Design vorzuziehen sei. Unsere Empfehlung ist, trotz dieses Befundes, so weit als möglich den Fisherschen Prinzipien zu folgen (Rundfeldt, 1953; John & Williams, 1995; Bailey, 2008). Im vorliegenden Fall würde dies weiterhin natürlich zur Empfehlung einer randomisierten vollständigen Blockanlage führen. Wir werden aber die Design-Frage im Folgenden wieder aufgreifen, wenn wir die Erweiterung der Mischerlichschen Gleitmethode auf den zweidimensionalen Fall betrachtet haben.
Im vorangegangenen Abschnitt haben wir gesehen, dass die Korrekturmethode von Mitscherlich mit einem geostatistischen Modell in Verbindung gesetzt werden kann, bei dem die Kovarianz mit der Distanz abnimmt. Dabei wird bei Mitscherlich davon ausgegangen, dass die Parzellen in einer einzigen Reihe angeordnet sind. Wenn die Parzellen in Zeilen und Spalten angeordnet sind, kann auch eine zweidimensionale Erweiterung des Modells verwendet werden. Insbesondere kann angenommen werden, dass die Kovarianz in Richtung der Zeilen und in Richtung der Spalten mit der Distanz abnimmt. Hierfür gibt es zahlreiche Modelle, die hier in ihrer Gänze nicht im Detail erörtert werden sollen (Gilmour et al., 1997; Piepho & Williams, 2010; Rodríguez-Álvarez et al., 2018). Auf den hier besonders relevanten Spezialfall eines linearen Modells kommen wir jedoch gleich noch zu sprechen.
von Boguslawski (1942) hat die Mitscherlich-Methode auf zwei Dimensionen erweitert, wobei er von einer zweifaktoriellen Behandlungsstruktur ausgeht. In seinem Beispiel werden v1 Stufen des einen Faktors systematisch in den Zeilen eines Blocks angeordnet und die v2 Stufen des anderen Faktors systematisch in den Spalten eines Blocks. Der gleitende Block hat somit v1 Zeilen und v2 Spalten. Die Gesamtzahl der Behandlungen, und daher auch die Gesamtzahl der Parzellen je Block haben die Größe v = v1 × v2. Ein bei von Boguslawski (1942) angegebenes Beispiel für zwei Faktoren mit jeweils vier Stufen und sechs Wiederholungen ist in Abb. 3 reproduziert.

Abb. 3. Anlageschema zur Ertragsflächenmethode von von Boguslawski (1942, Abb. 1). Faktor 1 hat die vier Stufen I-IV (v1 = 4), Faktor 2 hat die vier Stufen 1–4 (v2 = 4).
Betrachten wir nun eine zweidimensionale Erweiterung des eindimensionalen Ansatzes für die Mitscherlich-Methode. Hierbei können alle denkbaren gleitenden Blöcke der Dimension v1 × v2 berücksichtigt werden. Diese finden wir, wenn oben links in der Anlage beginnend der gleitende Block schrittweise von links nach rechts jeweils um eine Spalte weitergerückt wird und darüber hinaus eine schrittweise Verschiebung Zeile für Zeile von oben nach unten erfolgt. Sodann kann für jedes Parzellenpaar in der Anlage abgezählt werden, wie viele gleitende Blöcke beide Parzellen gemeinsam haben. Wird dann wie im eindimensionalen Fall angenommen, dass die Blöcke unabhängige Effekte mit Varianz 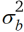 haben, ergibt sich die folgende Kovarianz-Struktur:
haben, ergibt sich die folgende Kovarianz-Struktur:
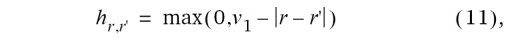
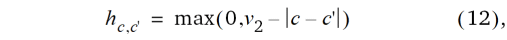
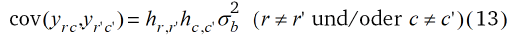
wobei yrc der Beobachtungswert in der r-ten Zeile und c-ten Spalte ist. Diese Kovarianzstruktur ist in der Geostatistik keine übliche, aber sie kann trotzdem mit der REML Methode angepasst werden.
Wir haben dieses Modell für das bei von Boguslawski (1942) angegebene Beispiel, welches in Abb. 3 und Abb. 4 reproduziert ist, angepasst und mit gängigen Alternativen [AR(1)-Modell, Modell mit unabhängigen Fehlern, Modell einer Blockanlage] verglichen (Abb. 5). In diesem Fall passen beispielsweise das autoregressive AR(1)-Modell und das Modell für eine Blockanlage besser als das lineare Modell (Gleichungen 11 bis 13) gemäß des AIC-Wertes.
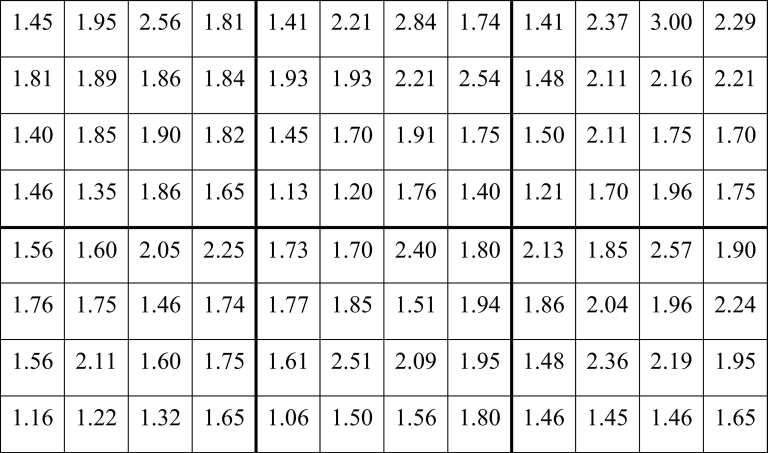
Abb. 4. Beispiel eines Mohnversuchs (1940) zur Ertragsflächenmethode von von Boguslawski (1942, Abb. 2) (zweites Beispiel). Die Behandlungen entsprechen der Struktur in Abb. 3. Kornerträge bei 92 % Trockensubstanz in kg/Teilstück; Teilstückgröße 4 m × 4 m = 16 qm.
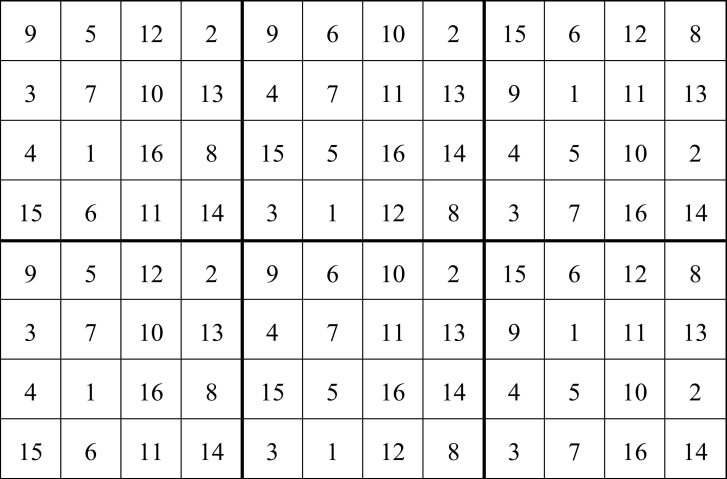
Abb. 5. Anlageschema für ein Design in 8 Zeilen und 12 Spalten mit 16 Behandlungen. D-effizientes Design unter Annahme des linearen geostatistischen Modells (13), angepasst für die Daten aus dem zweiten Beispiel (Tab. 5), erzeugt mit der SAS Prozedur OPTEX (Piepho, 2015).
Tab. 5. Parameterschätzwerte (REML) für das lineare geostatistische Modell in Gleichung (13) sowie weitere Modelle [AR(1)-Modell, Modell einer Blockanlage, Modell mit unabhängigen Fehlern] für das zweite Beispiel.
Parameter/ | LINa | AR(1)b | AR(1) ⊗ AR(1)c | Blockanlaged | Unabhängige Fehlere |
| – | 0.05414 | 0.05409 | – | – |
| 0.000447 | – | – | 0.006154 | – |
| 0.2500 | 0.1995 | 0.1794/0.2432 | – | – |
| 0.04595 | 0 | 0 | 0.04811 | 0.05427 |
Devianz | 19.3 | 16.7 | 15.6 | 18.5 | 22.6 |
AIC | 23.3 | 20.7 | 21.6 | 22.5 | 24.6 |
a Kovarianz-Struktur in Gleichung (13). | |||||
Basierend auf dem linearen geostatistischen Modell (13) haben wir wieder jeweils mittels A-Effizienz und D-Effizienz ein Design erzeugt. Hierbei sind wir von v = 16 Behandlungen ausgegangen, ohne eine zweifaktorielle Struktur speziell zu berücksichtigen. Mit der SAS Prozedur OPTEX, welche die D-Effizienz als Suchkriterium verwendet, wurde das Design in Abb. 5 gefunden, während die computergestützte Suche nach einem A-effizienten Design das Ergebnis in Abb. 6 lieferte. Interessanterweise zeigen beide Designs eine sehr ähnliche Systematik wie Abb. 3. Alle drei Designs haben sehr ähnliche Effizienzen (Tab. 6), wobei bemerkenswerterweise das Design in Abb. 3 eine leicht bessere D-Effizienz hat als das beste mit der SAS Prozedur OPTEX gefundene Design in Abb. 5. Zwar wiederholen sich in Abb. 5 und Abb. 6 die 4 × 4 Blöcke in ihrem räumlichen Muster nicht perfekt, es ist aber in Abb. 5 und Abb. 6 wie in Abb. 2 so, dass jeder gleitende Block der Dimension 4 × 4 jeweils alle 16 Behandlungen umfasst.
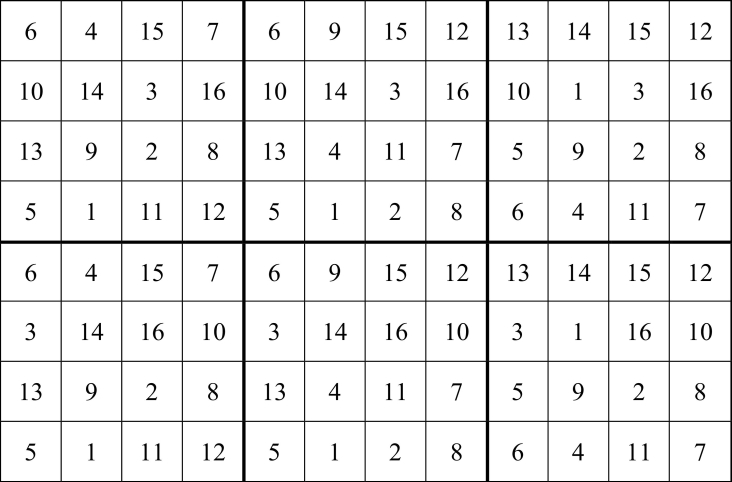
Abb. 6. Anlageschema für ein Design in 8 Zeilen und 12 Spalten mit 16 Behandlungen. A-effizientes Design unter Annahme des linearen geostatistischen Modells (13), angepasst für die Daten aus dem zweiten Beispiel (Tab. 5), erzeugt mit einem in Julia selbst geschriebenen Programm (Vo-Thanh & Piepho, 2020).
Tab. 6. Durchschnittliche Varianz und D-Effizienz der Versuchspläne in Abb. 3, Abb. 5 und Abb. 6.
Versuchsplan | Durchschnittliche Varianza | D-Effizienzb |
Abb. 3 | 0.0158807 | 104.825 |
Abb. 5 | 0.0158707 | 104.798 |
Abb. 6 | 0.0158678 | 104.816 |
a Durchschnittliche Varianz einer paarweisen Differenz der 16 Behandlungen (kleiner ist besser); steht in monotoner Beziehung zur A-Effizienz | ||
Es sei auch hier betont, dass die Designs in Abb. 5 und Abb. 6 ein spezielles Kovarianzmodell voraussetzen und dass es in der Praxis nicht zu erwarten ist, dass genau dieses Modell gut zu den Daten passen wird. Daher wäre dieses Design nicht unbedingt zu empfehlen. Es gibt natürlich viele Alternativen, von denen eine in Abb. 7 gezeigt ist. Dieses randomisierte Design folgt einem auflösbaren Zeilen-Spalten-Plan mit sechs vollständigen Wiederholungen. Es ist außerdem in den Zeilen latinisiert, was bedeutet, dass keine Behandlung mehr als einmal vorkommt. In diesem Fall ist es sogar so, dass jede Zeile einen vollständigen Block bildet. Außerdem bilden jeweils zwei benachbarte Spalten, also die Spalten 1 und 2, 3 und 4, usw., einen vollständigen Block. Dies wird als t-Latinisierung bezeichnet. Desweiteren ist dieses Design hinsichtlich der räumlichen Nachbarschaft von Behandlungen optimiert. Für die Designoptimierung wird ein lineares Modell zugrundegelegt, welches neben Behandlungseffekte nur Effekte für die verschiedenen disjunkten Blockeinheiten umfasst, aber keine geostatistische Kovarianzstruktur wie bei den Designs in Abb. 5 und Abb. 6. Nähere Details zu dieser Art von Design finden sich in Piepho et al. (2015a) und Piepho et al. (2020).
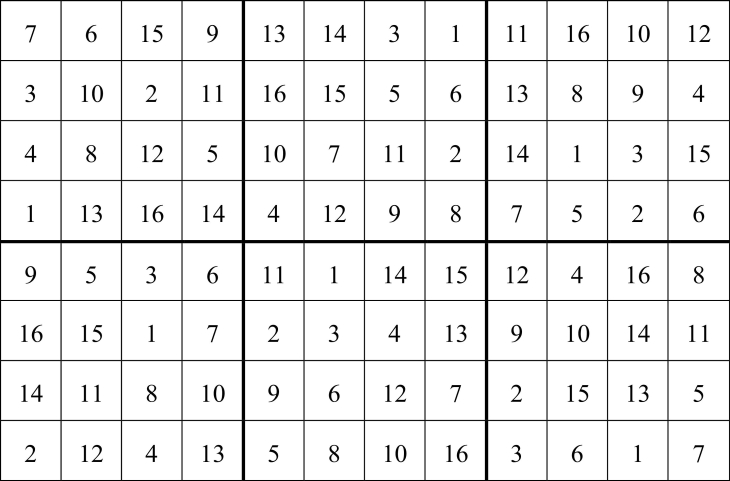
Abb. 7. Anlageschema für ein A-optimales Design in 8 Zeilen und 12 Spalten mit 16 Behandlungen. Auflösbarer Plan mit 6 Wiederholungen, Latinisierung in den Zeilen und t-Latinisierung in jeweils t = 2 Spalten, erzeugt mitCycDesigN 7.0 (VSNi; https://www.vsni.co.uk/software/cycdesign).
In dieser Arbeit wurde ein geostatistisches Modell hergeleitet, das mit dem Verfahren der Gleitmethode von Mitscherlich und deren Erweiterung von von Boguslawski in Einklang steht, indem für jeden gleitenden Block ein zufälliger Blockeffekt im Modell vorhanden ist. Dieser Blockeffekt induziert eine Kovarianzstruktur, die ähnlich ist zu einer ganzen Klasse von sog. geostatistischen Kovarianzstrukturen, die heutzutage leicht mittels Softwarepaketen für lineare gemischte Modelle angepasst werden können.
Eine Betrachtung der an die Daten von zwei Beispielen angepassten Kovarianzstrukturen im Rahmen einer Erzeugung optimaler Versuchsanlagen führte zu dem überraschenden Befund, dass das systematische Versuchsdesign von Mitscherlich und mit Abstrichen auch das von von Boguslawski optimal unter diesem angenommenen Modell sind. Insofern führt das vorgeschlagene geostatistische Modell zu einer Kohärenz von Versuchsplan und Auswertung dieser Anlagen. Allerdings ist nicht davon auszugehen, dass dieses Modell notwendigerweise immer optimal an gegebene Daten passt, so dass für zukünftige Versuche nicht der Schluss gezogen werden kann, systematische Versuchsdesigns seien grundsätzlich zu empfehlen. Vielmehr ist es aus unserer Sicht empfehlenswert, einen randomisierten Versuchsplan zu verwenden (Rundfeldt, 1953). Einer der großen Vorteile eines randomisierten Versuchsplanes ist, dass die Randomisationsstruktur ein auf jeden Fall zulässiges Analysemodell induziert, welches als Baseline-Modell bezeichnet werden kann (Piepho & Williams, 2010). Ein solches Modell lässt darüber hinaus verschiedene Auswertungsmöglichkeiten offen, einschließlich der Einbeziehung einer geostatistischen Kovarianzstruktur. Likelihood-basierte Kriterien wie die Devianz und das AIC können dann herangezogen werden, um zu entscheiden, ob eine geostatistische Modellierung sinnvoll ist und wenn ja, welche Kovarianzstruktur am besten zu den Daten passt. Einschränkend muss hinzugefügt werden, dass bei Verwendung desselben Datensatzes zur Modellselektion die Signifikanztests einer anschließenden Analyse mit dem ausgewählten Modell das nominelle Signifikanzniveau oft nicht einhalten (Richter et al., 2015).
Für bereits vorliegende Versuche, die nach einem systematischen Design angelegt wurden, liefert das hier vorgeschlagene Modell ebenfalls eine mögliche Auswertungsoption, aber nicht die einzige. Wegen der fehlenden Randomisation kann jedoch kein Baseline-Modell formuliert werden, welches mit einer Randomisation begründet werden könnte. Man könnte versucht sein, das hier angegebene lineare geostatistische Modell als Baseline-Modell zu verstehen. Diesem Eindruck möchten wir aus verschiedenen Gründen entgegentreten. Zum einen könnte durch so eine Betrachtungsweise der falsche Eindruck entstehen, eine systematische Versuchsanlage sei auf jeden Fall vertretbar, weil es ja ein solches Modell gibt. Zum anderen muss berücksichtigt werden, dass ein Paradigmenwechsel erfolgt in dem Moment, wo eine geostatistische Analyse erwogen wird (Piepho et al., 2013). Wie oben betont, induziert eine Randomisation in der Regel ein ganz bestimmtes Analysemodell, welches immer verwendet werden kann. In dem Moment aber, wo eine geostatistische Modellierung erfolgt, wird diese Basis verlassen. Stattdessen wird die Annahme getroffen, die Daten seien nach einem noch zu identifizierenden geostatistischen Modell erzeugt worden. Die große Herausforderung ist dann, das jeweils beste geostatistische Modell zu identifizieren, und zwar aus einer potentiell sehr großen Klasse von Modellen, wobei dann immer die Unsicherheit bleibt, ob tatsächlich das beste Modell gefunden wurde. All diese Komplikationen treten dann nicht auf, wenn ein Versuch randomisiert wurde, weil dann immer das Baseline-Modell zur Verfügung steht. Dieses kann zwar geostatistisch erweitert werden, muss es aber nicht. Bei systematischen Versuchsanlagen besteht dagegen wegen des Fehlens eine Baseline-Modells die Notwendigkeit, verschiedene Modelle auszuprobieren, einschließlich geostatistischer Optionen, und das jeweils beste zu identifizieren. Dabei bleibt immer die Unsicherheit, ob auch das beste Modell gefunden werden konnte und ob es wegen der systematischen Anlage nicht zu verzerrten Schätzungen von Behandlungseffekten kommt.
Wir sind dankbar für zwei Gutachten, die uns sehr geholfen haben, die Klarheit der Darstellung zu verbessern. Unser ganz besonderer Dank gilt Herrn Professor Dr. Jochen Alkämper, dem Betreuer der Diplomarbeit des Erstautors, ohne den diese Arbeit nicht entstanden wäre. Er hat bei Aufräumarbeiten eine Ablichtung der Arbeit von von Boguslawski (1942) aufgefunden, die er dankenswerterweise dem Erstautor zur Verfügung stellte. Als Schüler von von Boguslawski hat er mehrere Versuche nach dessen Ertragsflächenmethode angelegt, unter anderem für seine Promotion (Alkämper, 1957). Aus heutiger Sicht besonders erwähnenswert ist der große Rechenaufwand bei der Auswertung, insbesondere auch nach der von von Boguslawski vorgeschlagenen Methode. Hierzu ein Zitat aus dem Brief an den Erstautor bei Übersendung des Artikels: „Es war eine ungeheure Rechnerei, und das noch mit Rechenschieber oder Rechenwalze. Meine Versuche hatten meist 36 Varianten!“
Die Autoren erklären, dass keine Interessenskonflikte vorliegen.
Alkämper, J., 1957: Die Komplexwirkung von Gründüngung und Stickstoff auf Ertragsbildung und Boden. Dissertationsschrift. Justus-Liebig-Universität Giessen.
Bailey, R.A., 2008: Design of comparative experiments. Cambridge University Press, Cambridge.
Cullis, B.R., A. Smith, N., Coombes, 2006: On the design of early generation variety trials with correlated data. Journal of Agricultural Biological and Environmental Statistics 11, 381-393, DOI: 10.1198/108571106X154443.
Fisher, R.A., 1925: Statistical methods for research workers. Oliver & Boyd, Edinburgh.
Gilmour, A.R., B.R. Cullis, A.P. Verbyla, 1997: Accounting for natural and extraneous variation in the analysis of field experiments. Journal of Agricultural Biological and Environmental Statistics 2, 269-293, DOI: 10.2307/1400446.
John, J.A., E.R. Williams, 1995: Cyclic and computer generated designs. Chapman & Hall, London.
Macholdt, J., H.P. Piepho, B. Honermeier, 2019: Does fertilization impact production risk and yield stability across an entire crop rotation? Insights from a long-term experiment. Field Crops Research 238, 82-92, DOI: 10.1016/j.fcr.2019.04.014.
Macholdt, J., E.M. Styczen, A. Macdonald, H.P. Piepho, B. Honermeier, 2020: Long-term analysis from a cropping system perspective: Yield stability, environmental adaptability, and production risk of winter barley. European Journal of Agronomy 117, 126056, DOI: 10.1016/j.eja.2020.126056.
Mitscherlich, E.A., 1925: Vorschriften zur Anstellung von Feldversuchen in der landwirtschaftlichen Praxis. 2. Auflage. Verlag Paul Parey, Berlin.
Möller-Arnold, E., Feichtinger, E., 1929: Der Feldversuch in der Praxis. Verlag Julius von Springer, Wien.
Nelder, J.A., 1965: The analysis of randomized experiments with orthogonal block structure. I. Block structure and the null analysis of variance. II. Treatment structure and the general analysis of variance. Proc. R. Soc. Lond. A 283, 147-178, DOI: 10.1098/rspa.1965.0012.
Piepho, H.P., 2015: Generating efficient designs for comparative experiments using the SAS procedure OPTEX. Communications in Biometry and Crop Science 10, 96-114.
Piepho, H.P., V. Michel, E.R. Williams, 2015a: Beyond Latin squares: A brief tour of row-column designs. Agronomy Journal 107, 2263-2270, DOI: 10.2134/agronj15.0144.
Piepho, H.P., J. Möhring, M. Pflugfelder, W. Hermann, E.R. Williams, 2015b: Problems in the parameter estimation for power and AR(1) models of spatial correlation in designed field experiments. Communications in Biometry and Crop Science 10, 3-16.
Piepho, H.P., J. Möhring, E.R. Williams, 2013: Why randomize agricultural experiments? Journal of Agronomy and Crop Science 199, 374-383, DOI: 10.1111/jac.12026.
Piepho, H.P., C. Richter, E.R. Williams, 2008: Nearest neighbour adjustment and linear variance models in plant breeding trials. Biometrical Journal 50, 164-189, DOI: 10.1002/bimj.200710414.
Piepho, H.P., E.R. Williams, 2010: Linear variance models for plant breeding trials. Plant Breeding 129, 1-8, DOI: 10.1111/j.1439-0523.2009.01654.x.
Piepho, H.P., E.R. Williams, V. Michel, 2020: Generating row-column field experimental designs with good neighbour balance and evenness of distribution of treatment replications. Journal of Agronomy and Crop Science (eingereicht).
Richter, C., B. Kroschewski, H.P. Piepho, J. Spilke, 2015: Treatment comparisons in agricultural field trials accounting for spatial correlation. Journal of Agricultural Science 153, 1187-1207.
Rodríguez-Álvarez, M.X., M.P. Boer, F.A. van Eeuwijk, P.H.C. Eilers, 2018: Correcting for spatial heterogeneity in plant breeding experiments with P-splines. Spatial Statistics 23, 52–71, DOI: 10.1016/j.spasta.2017.10.003.
Rundfeldt, H., 1953: Die Prüfung der wichtigsten Verfahren im Feldversuchswesen an hand von Modellen. Zeitschrift für Pflanzenzüchtung 32, 301-354.
Schabenberger, O., C.A. Gotway, 2005: Statistical methods for spatial data analysis. Chapman & Hall, Boca Raton.
Slaets, J., R. Boeddinghaus, H.P. Piepho, 2020: Linear mixed models and geostatistics for designed experiments in soil science – two entirely different methods or two sides of the same coin? European Journal of Soil Science, DOI: 10.1111/ejss.12976.
Thomas, E., 2006: Feldversuchswesen. Ulmer, Stuttgart.
von Boguslawski, E., 1942: Die „Ertragsflächenmethode“ zur gegenseitigen Abstufung von zwei Untersuchungsfaktoren im Feldversuch. Pflanzenbau 18, 129-149.
von Lochow, J., W. Schuster, 1961: Anlage und Auswertung von Feldversuchen: Anleitungen und Beispiele für die Praxis der Versuchsarbeit. DLG-Verlag, Frankfurt.
Vo-Thanh, N., H.P. Piepho, 2020: An update formula for generating experimental designs under an analysis of variance model (eingereicht).
Wermke, M., 1959: Zur Erfassung der Bodenunterschiede im Feldversuch. I. Teil: Gleitverfahren und Varianzanalyse. Zeitschrift für landwirtschaftliches Versuchs- und Untersuchungswesen 5, 255-272.
Williams, E.R., 1986: A neighbour model for field experiments. Biometrika 73, 279-287, DOI: 10.2307/2336204.
Williams, E.R., H.P. Piepho, 2013: A comparison of spatial designs for field variety trials. Australian and New Zealand Journal of Statistics 55, 253-258, DOI: 10.1111/anzs.12034.
Wolfinger, R.D., 1996: Heterogeneous variance-covariance structures for repeated measures. Journal of Agricultural Biological and Environmental Statistics 1, 205-230, DOI: 10.2307/1400366.